分组查询注意力 (Grouped Query Attention) 是一种在大型语言模型中的多查询注意力 (MQA) 和多头注意力 (MHA) 之间进行插值的方法,它的目标是在保持 MQA 速度的同时实现 MHA 的质量。
这篇文章中,我们将解释GQA的思想以及如何将其转化为代码。
GQA是在论文 GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints paper.中提出,这是一个相当简单和干净的想法,并且建立在多头注意力之上。
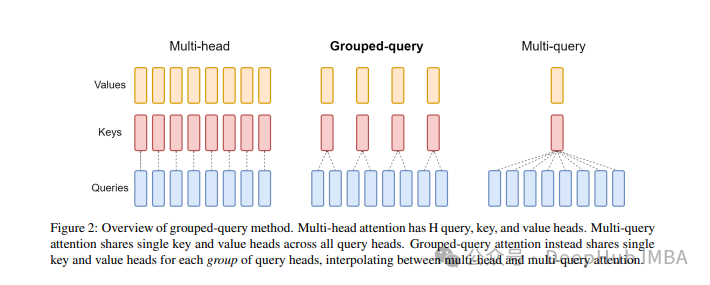
GQA
标准多头注意层(MHA)由H个查询头、键头和值头组成。每个头都有D个维度。Pytorch的代码如下:
fromtorch.nn.functionalimportscaled_dot_product_attention
# shapes: (batch_size, seq_len, num_heads, head_dim)
query=torch.randn(1, 256, 8, 64)
key=torch.randn(1, 256, 8, 64)
value=torch.randn(1, 256, 8, 64)
output=scaled_dot_product_attention(query, key, value)
print(output.shape) # torch.Size([1, 256, 8, 64])对于每个查询头,都有一个对应的键。这个过程如下图所示:
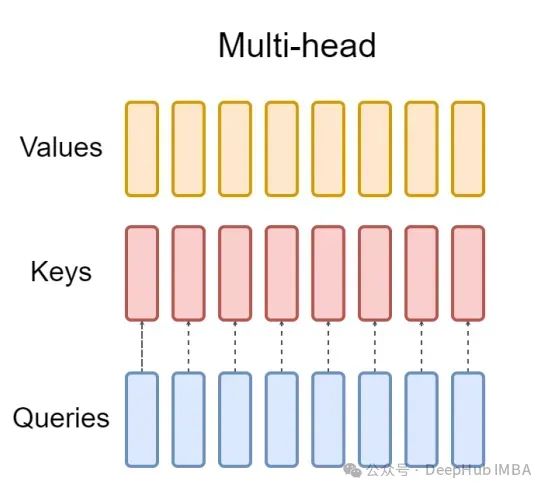
而GQA将查询头分成G组,每组共享一个键和值。可以表示为:
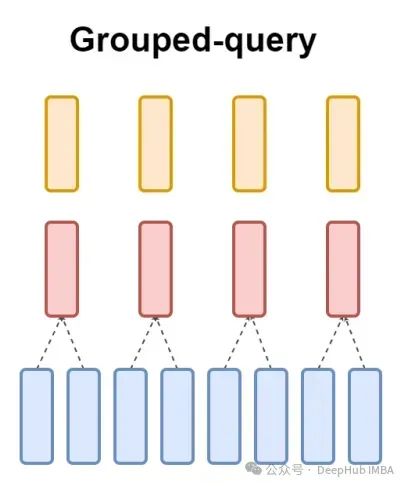
使用可视化的表示就能非常清楚的了解GQA的工作原理,就像我们上面说的那样,GQA是一个相当简单和干净的想法
Pytorch代码实现
让我们编写代码将这种将查询头划分为G组,每个组共享一个键和值。我们可以使用einops库有效地执行对张量的复杂操作。
首先,定义查询、键和值。然后设置注意力头的数量,数量是随意的,但是要保证num_heads_for_query % num_heads_for_key = 0,也就是说要能够整除。我们的定义如下:
importtorch
# shapes: (batch_size, seq_len, num_heads, head_dim)
query=torch.randn(1, 256, 8, 64)
key=torch.randn(1, 256, 2, 64)
value=torch.randn(1, 256, 2, 64)
num_head_groups=query.shape[2] //key.shape[2]
print(num_head_groups) # each group is of size 4 since there are 2 kv_heads为了提高效率,交换seq_len和num_heads维度,einops可以像下面这样简单地完成:
fromeinopsimportrearrange
query=rearrange(query, "b n h d -> b h n d")
key=rearrange(key, "b s h d -> b h s d")
value=rearrange(value, "b s h d -> b h s d")然后就是需要在查询矩阵中引入”分组“的概念。
fromeinopsimportrearrange
query=rearrange(query, "b (h g) n d -> b g h n d", g=num_head_groups)
print(query.shape) # torch.Size([1, 4, 2, 256, 64])上面的代码我们将二维重塑为二维:对于我们定义的张量,原始维度8(查询的头数)现在被分成两组(以匹配键和值中的头数),每组大小为4。
最后最难的部分是计算注意力的分数。但其实它可以在一行中通过insum操作完成的
fromeinopsimporteinsum, rearrange
# g stands for the number of groups
# h stands for the hidden dim
# n and s are equal and stands for sequence length
scores=einsum(query, key, "b g h n d, b h s d -> b h n s")
print(scores.shape) # torch.Size([1, 2, 256, 256])scores张量和上面的value张量的形状是一样的。我们看看到底是怎么操作的
einsum帮我们做了两件事:
1、一个查询和键的矩阵乘法。在我们的例子中,这些张量的形状是(1,4,2,256,64)和(1,2,256,64),所以沿着最后两个维度的矩阵乘法得到(1,4,2,256,256)。
2、对第二个维度(维度g)上的元素求和——如果在指定的输出形状中省略了维度,einsum将自动完成这项工作,这样的求和是用来匹配键和值中的头的数量。
最后是注意分数与值的标准乘法:
importtorch.nn.functionalasF
scale=query.size(-1) **0.5
attention=F.softmax(similarity/scale, dim=-1)
# here we do just a standard matrix multiplication
out=einsum(attention, value, "b h n s, b h s d -> b h n d")
# finally, just reshape back to the (batch_size, seq_len, num_kv_heads, hidden_dim)
out=rearrange(out, "b h n d -> b n h d")
print(out.shape) # torch.Size([1, 256, 2, 64])这样最简单的GQA实现就完成了,只需要不到16行python代码:
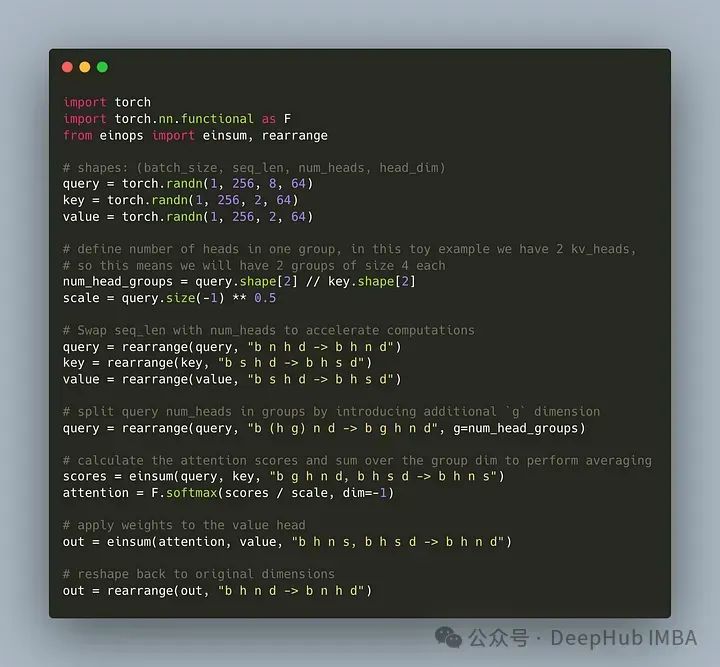
最后再简单提一句MQA:多查询注意(MQA)是另一种简化MHA的流行方法。所有查询将共享相同的键和值。原理图如下:
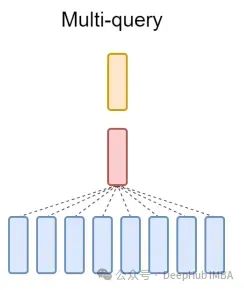
可以看到,MQA和MHA都可以从GQA推导出来。具有单个键和值的GQA相当于MQA,而具有与头数量相等的组的GQA相当于MHA。
GQA的好处是什么?
GQA是最佳性能(MQA)和最佳模型质量(MHA)之间的一个很好的权衡。
下图显示,使用GQA,可以获得与MHA几乎相同的模型质量,同时将处理时间提高3倍,达到MQA的性能。这对于高负载系统来说可能是必不可少的。
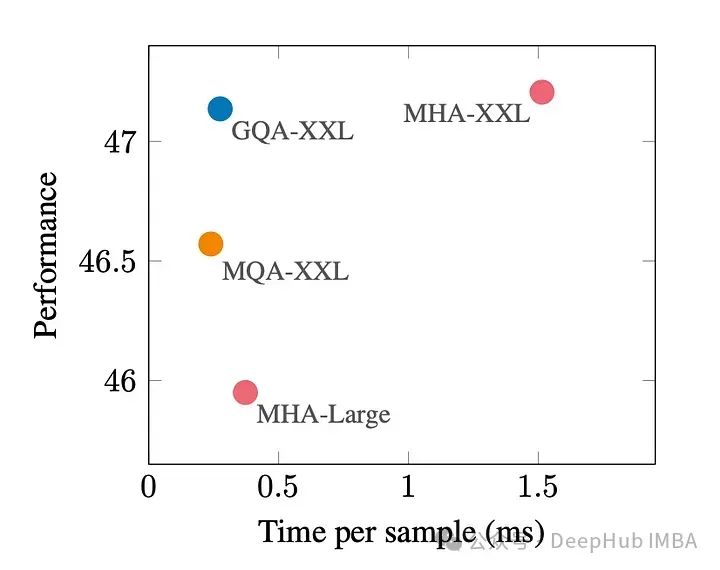
在pytorch中没有GQA的官方实现。所以我找到了一个比较好的非官方实现,有兴趣的可以试试:
https://avoid.overfit.cn/post/58ee0d8f5ed14414bc856080ab748047


