- 方向导数作为标量量,表征了函数在特定方向上的变化率。其数学表示为 ∇ᵤf(x) 或 Dᵤf(x)。
- 对于标量函数 f(x): Rⁿ → R,其梯度由函数的偏导数构成向量场。梯度向量指向函数值增长最快的方向,其模长等于该方向的方向导数。
- 方向导数的计算可通过两种方法实现:其一是引入函数 g(s) = f(x + su),方向导数即为 g′(0);其二是利用方向导数等于梯度与方向向量点积的性质:∇ᵤf(x) = ∇f(x)u。
引论
函数在不同方向上的变化特性分析在诸多领域具有重要意义,典型应用如神经网络中利用梯度更新权重的训练过程。本文将系统探讨方向导数与梯度的理论基础,并通过如下等式阐述二者的内在联系:
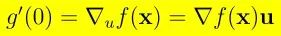
本文的理解需要读者具备点积、导数、莱布尼茨与拉格朗日记号、偏导数以及链式法则等基础数学知识。
方向导数与梯度的基本定义
首先考察单变量函数的导数定义:
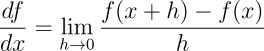
(此处采用莱布尼茨记号 df/dx 表示导数,这是拉格朗日记号 f′(x) 的等价表示。)单变量函数 f(x) 的导数表征了函数的斜率,定义为函数值的增量与自变量无穷小增量的比值。它描述了在给定点处当参数发生无穷小变化时函数值的变化率,从而反映了函数在该点的增减性质和变化剧烈程度。
梯度的数学表述
梯度是导数概念在标量值函数 f(x): Rⁿ → R(多输入单输出映射)上的推广,其定义为:
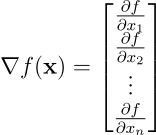
梯度作为标量值函数的重要特征量,是由所有偏导数组成的向量(通常表示为列向量)。
从本质上看,梯度是所有偏导数的有序集合。(向量在此作为空间点坐标的有序数组,具有大小和方向两个基本特征。)算子符号 ∇(希腊字母 nabla,读作"del")可视为作用于函数的微分算子。梯度向量的每个分量表示函数对应变量的偏导数:δf/δx₁ 表征了函数关于 x₁ 的变化率,此时将其他变量(x₂, ...xₙ)视为常数。梯度的一个核心性质是其指向函数值增长最快的方向,这一性质的严格证明将在第 6 节中给出。
方向导数的理论基础
方向导数通常表示为 ∇ᵤf(x) 或 Dᵤf(x),本文采用前者。其严格数学定义如下:
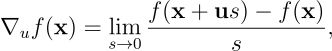
在此定义中,u 表示单位向量,其模长恒为 1。向量的模长定义为各分量平方和的平方根,数学上用双竖线表示(某些文献中采用单竖线):
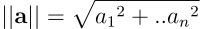
其中 a ∈ Rⁿ。方向导数的定义形式与单变量导数具有显著的相似性。(本文使用变量 s 而非 h,以突出其与单变量情况的区别。)方向导数的关键特征在于其输入形式 x + su 构成了一个直线方程。这表示从向量 x 出发,沿 u 方向移动 s 个单位长度。该表达式实质上研究了函数在 u 方向上的无穷小变化特性。方向导数量化了函数在给定点沿特定方向发生无穷小位移时的变化率。这一概念通过记号 ∇ᵤf(x) 得到精确表达,其中 u 作为下标标识方向特征。
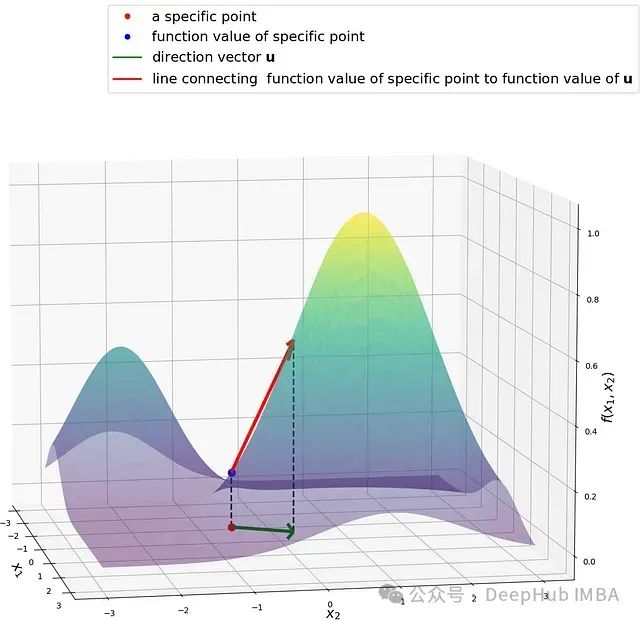
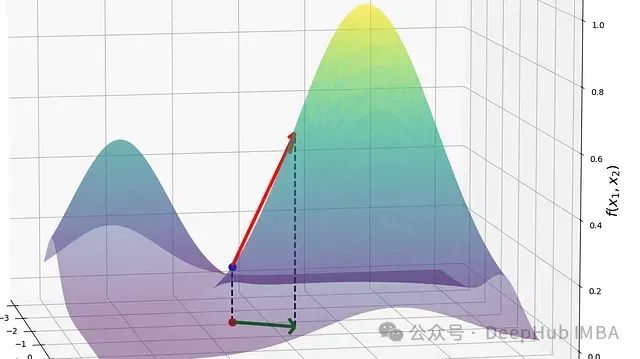
图 1:二维空间中的函数输入点(红点)与其沿方向向量(绿线 su)的变化示意。方向导数表征了当沿 u 方向发生无穷小位移(s → 0)时函数值的瞬时变化率。
为深入理解这一概念,上图所示的几何展示了一个二维函数,平面上的红点代表特定输入点,其函数值由蓝点标识。对比单变量函数仅能沿自变量方向变化的情况,多变量函数的输入可在各个方向发生变化。例如可以在 x₁ 方向移动一个单位,同时在 x₂ 方向移动两个单位。要准确描述函数值的变化特性,首先需要明确运动方向。图中绿色向量即表示这一方向。该向量实质上是 su,其中标量 s 确定了移动距离,可理解为对方向向量 u 的尺度调节。
这种构造使得方向导数的概念自然地扩展了单变量导数的思想。它描述了函数在指定方向上的瞬时变化率。当绿色向量趋于无穷小时(s → 0),其对应了函数在该点处沿特定方向的切线。这条切线的斜率即为方向导数的几何意义。
这一数学概念可通过一个实际的类比来理解:设想在起伏不平的山地地形(函数)上进行导航。方向导数相当于在特定位置沿给定方向探测地形的变化程度,这对于确定安全的运动路径具有重要意义。
梯度与方向导数的关联性
梯度与方向导数虽然表征了函数的不同性质,但二者存在密切的内在联系。梯度作为向量量,指示了函数值增长最快的方向;而方向导数作为标量量,量化了函数在特定方向上的变化率。当所选方向与最速上升方向重合时,方向导数的值等于梯度的模长,方向导数可表示为梯度与方向向量的内积。下表系统总结了二者的主要特征及关联。

梯度与方向导数的特征对比
方向导数的计算理论
下面我们将严格证明如下核心等式:
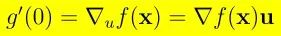
为确保论证的严密性,我们将分步进行推导。
极限定义与导数的基本原理
方向导数的本质是函数在特定点沿给定方向的无穷小变化率。这一概念已在等式 2 中通过极限形式得到严格定义。从几何观点看,这一极限过程可理解为在函数曲面上选取两个点(如图 1 所示),通过使其中一点逐渐接近感兴趣点来确定变化率。对于多变量函数,这种极限过程仅在点的运动严格限制在由 su 确定的直线上时才具有明确意义。
这一概念可以通过另一个数学视角来理解:由于 x 和 u 为固定向量,参数 s 成为唯一的自由变量。表达式 x + su 实质上定义了一条参数化直线,而函数 f 则将该直线上的每一点映射到对应的函数值。下图提供了这一概念的直观展示,其中展示了原图的局部放大区域。图中标注了直线 su 上的若干离散点及其对应的函数值。这种构造实质上定义了一个关于参数 s 的单变量函数。根据导数的基本定义,该函数在各点的导数表征了相应位置的变化率。在 s = 0 处的导数恰好对应于原函数在给定方向上的方向导数。
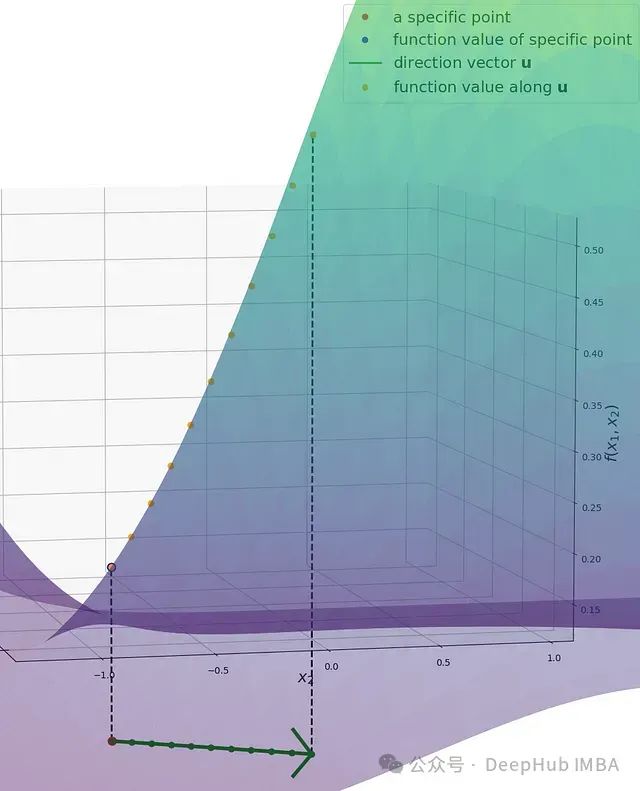
图 2:参数化直线 x + su 上的点(绿点)与其函数值 f(x + su) (橙点)之间的映射关系。这一构造定义了参数 s 的函数 g(s)=f(x + su)。带有黑色边框的橙色点表示 g(s) 在 s=0 处的导数,即函数 f 在点 x 沿方向向量 u 的方向导数。
第一部分:g′(0) = ∇ᵤf(x) 的证明
基于上述分析,我们引入辅助函数 g(s) 将方向导数的计算转化为单变量函数的导数问题:
我们的目标是证明该辅助函数在 s=0 处的导数等于方向导数,即:
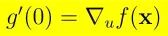
按照单变量函数导数的定义,对函数 g 关于参数 s 求导:
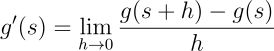
在 s=0 处取值:
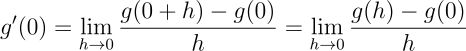
将 g 的定义式 g(s) = f(x + su) 代入。这里需要注意符号的精确含义:g 是关于参数 s 的函数。表达式 g(h) 表示将参数值取为 h,即 g(s = h)。因此可以在函数定义中用 h 替换 s,得到:g(s=h) = f(x + hu)。g(0) = f(x + 0u) = f(x)也是类似的,将其代入得到:
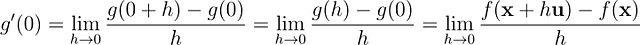
这一表达式与方向导数的定义形式完全一致,仅变量符号由 s 改为 h。由于极限运算与变量符号的选择无关,我们可以将变量重命名为 s:
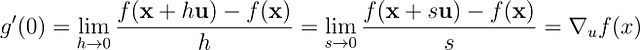
这样完成了预期结论的证明:
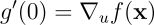
第二部分:∇ᵤf(x) = ∇f(x)u 的证明
在完成了第一部分的证明后,现在转向第二个关键等式的证明,即方向导数等于梯度与方向向量的内积:∇ᵤf(x) = ∇f(x)u。这一等式揭示了方向导数与梯度之间的本质联系。我们将继续利用前面引入的辅助函数 g(s),目标是证明:
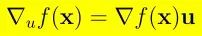
证明过程如下:
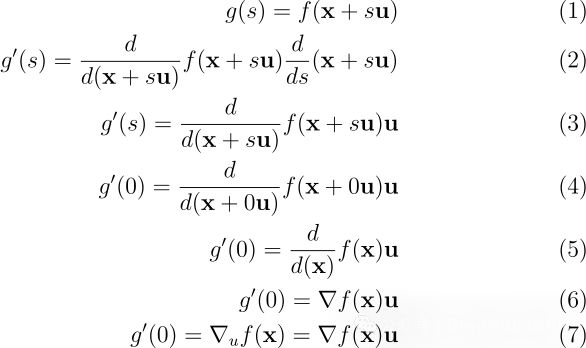
这个证明过程中的每个步骤都具有深刻的数学意义:
- 第 1 行应用了链式法则,这是复合函数求导的基本工具。
- 第 2 行利用了一个关键观察:x + su 关于 s 的导数恒等于方向向量 u。但外部导数必须保持符号形式,因为函数 f 的具体形式未知。
- 第 4 行将参数 s 取值为 0,这对应于我们感兴趣的特定点。
- 第 5 行计算了 s = 0 时的表达式值。这里需要特别注意一个常见的符号错误:d(x)/f(x) 的写法不准确。
- 第 6 行进行了关键的修正:由于 f 的输入是向量,其导数应当用梯度符号表示。
- 最后在第 7 行,应用了上节中证明的结论 g′(0) = ∇ᵤf(x),完成了证明。
梯度的最速上升性质
前文中提到了两个重要结论:
- 梯度指向函数值增长最快的方向
- 当方向与最速上升方向重合时,方向导数等于梯度的模长
下面我们将从数学角度严格证明这两个性质。
方向导数表征了函数在给定方向上的变化率。这个变化率在最陡峭的方向上达到最大值。使方向导数取得最大值的方向向量 u 即为最速上升方向。下面我们将证明这个方向恰好与梯度方向重合。
根据前面的证明,我们知道 ∇ᵤf(x) = ∇f(x)u。此式表明方向导数等于梯度与方向向量的内积。根据内积的基本定义:

其中 a, b ∈ Rⁿ,θ 表示向量 a 与 b 之间的夹角,双竖线表示向量的模长。由于 u 是单位向量,其模长为 1,因此:
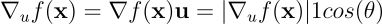
现在的问题转化为:何时这个表达式取得最大值?由于余弦函数的值域为[-1,1],该表达式在余弦值等于 1 时达到最大: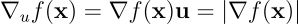
这一条件仅在 ∇f(x) 与 u 的夹角为 0 时成立,即两个向量指向相同方向。这证明了最速上升方向与梯度方向的一致性。同时在这种情况下方向导数确实等于梯度的模长,这是由于夹角余弦达到最大值 1 所致。
因此梯度指向最速上升方向这一性质是内积性质与优化理论的自然结果:当且仅当两个向量方向一致时,它们的内积(标准化后)达到最大值。
理论应用实例
为加深对前述理论的理解,下面通过两个具体算例进行说明。
实例分析:∇ᵤf(x) = ∇f(x)u
考虑函数 f(x) = x₁² + x₂² 在点(4,5)处的特性。我们需要解决两个问题:
- 确定在该点处最速上升的方向
- 计算该方向上的变化率
解析过程: 根据前述理论,最速上升方向由梯度确定。首先计算函数的梯度:
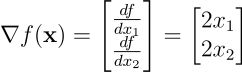
在点(4,5)处,最速上升方向由向量[8, 10]ᵗ 给出(此处上标 t 表示转置,由于排版原因将列向量写作行向量)。该方向上的变化率等于梯度的模长:
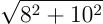
该实例直观地展示了梯度的方向特性和大小意义。
实例分析:g′(0) = ∇ᵤf(x)
这个实例源自参考文献[1]第 24 页的示例 2.3。考虑函数:
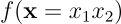
要求在点 x = [1, 0] 处沿方向 u = [−1, −1] 的方向导数。(原文中使用符号 s 表示方向向量,这里统一记为 u)。
解析过程: 这个问题可以通过计算梯度后与方向向量做内积来解决。但为了展示辅助函数方法的应用,构造函数:
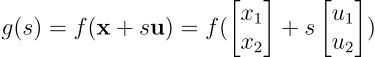
由于原函数形式为 f(x = x₁x₂),可得: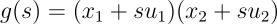
将点 x 和方向 u 的坐标代入:
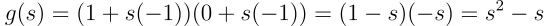
接下来计算 g 在 s=0 处的导数:
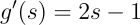
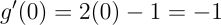
因此函数 f(x) = x₁x₂ 在点 x = [1, 0] 处沿方向 u = [−1, −1] 的方向导数为-1。
此例展示了如何通过构造辅助函数来计算方向导数,验证了理论分析的实用性。
理论要点总结
通过对方向导数与梯度的系统分析,可以得到以下核心结论:
- 方向导数作为标量量,度量了函数在特定方向上的变化率,其数学表示为 ∇ᵤf(x)。这一概念将单变量导数推广到了多维空间。
- 梯度作为向量量,是由函数各个偏导数构成的向量场。其两个基本性质是:- 指向函数值增长最快的方向- 其模长等于最速上升方向上的方向导数
- 方向导数的计算可通过两种等价途径实现:- 构造辅助函数 g(s) = f(x + su),方向导数等于 g′(0)- 计算梯度与方向向量的内积:∇ᵤf(x) = ∇f(x)u
这些理论成果在实际应用中具有重要意义,为函数局部性质的分析提供了有力工具。
参考文献
[1] Mykel J. Kochenderfer and Tim A. Wheeler. Algorithms for Optimization. The MIT Press, 2019. isbn: 0262039427.
[2] James Stewart. Calculus: Early Transcendentals. 8th. Cengage Learning, 2015. isbn: 978-1-305-25380-2.
https://avoid.overfit.cn/post/7bd19d5225cf4f908139e0178ae7d901


