大型语言模型在各个领域都展现出了卓越的性能,但其核心组件之一——softmax 注意力机制在计算资源消耗方面存在显著局限性。本文将深入探讨如何通过替代方案实现线性时间复杂度,从而突破这一计算瓶颈。
注意力机制基础理论
本文假设读者已经熟悉 ChatGPT、Claude 等模型及其底层的 transformer 架构原理。注意力机制是这类模型的核心组件。与传统循环神经网络(RNN)将历史信息压缩存储在固定维度的隐藏状态中不同,注意力机制能够直接访问和选择性利用历史信息。这种机制本质上是在每次预测时,根据当前查询动态检索最相关的历史信息。
transformer 架构中的注意力机制通过键(key)、查询(query)和值(value)三个嵌入向量实现信息的动态检索。具体而言 transformer 的注意力机制通过计算查询向量与所有键向量的相似度,获得注意力权重,再用这些权重对相应的值向量进行加权组合。这一计算过程可以形式化表示为:
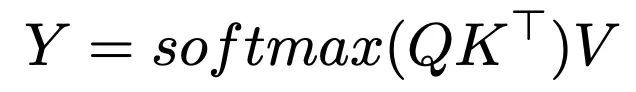
这种机制使模型能够在生成预测时有选择地利用整个上下文中的相关信息。在此过程中使用 softmax 函数的目的是将原始相似度分数转换为概率分布,这在本质上类似于 k 近邻机制,即相关性更高的键值对获得更大的权重。
下面我们分析单个注意力层的计算复杂度:
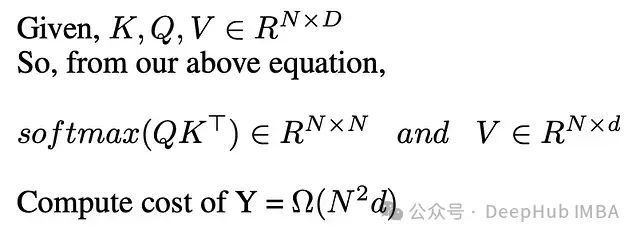
Softmax 机制的计算瓶颈
通过上述分析可以看出,标准注意力机制需要对 NxN 维度的矩阵执行 softmax 运算,这导致计算复杂度随序列长度呈二次方增长。虽然这种计算复杂度对于较短序列是可接受的,但在处理长度达到 100k 以上的序列时,计算效率会显著降低。
这一计算瓶颈促使研究者们思考:是否存在能够降低计算复杂度的替代方案?这就引出了线性注意力机制的研究。
线性注意力机制
Katharopoulos 等人提出了一种创新性的解决方案,他们通过将 softmax 指数函数重写为特征映射 φ(x)的点积形式的核函数,并利用矩阵乘法的结合律,成功将注意力计算重构为线性形式。这一转换过程如下图所示:

在该方法中 Katharopoulos 等人采用 elu(x) + 1 作为特征映射函数 φ(x)。任何能够有效近似指数相似度的核特征映射都可以作为候选函数。这种方法的计算复杂度可以表示为:

这种重构方法消除了计算完整 N×N 注意力矩阵的需求,将复杂度降低至 O(Nd²),其中 d 表示嵌入维度。在大型语言模型中,通常序列长度 N 远大于嵌入维度 d,因此这种方法实际上实现了线性时间复杂度。
从循环的角度来看线性注意力机制:

为什么这种转换在线性注意力中可行而在 softmax 中不可行呢?这是因为 softmax 函数本质上不可分离,无法分解为独立项的乘积。在解码阶段,由于只需要维护 d × d 维度的状态矩阵 S_(n-1),每个 token 的生成复杂度仅为 O(d²)。
但是这种计算效率的提升也带来了一个重要的局限性。由于状态矩阵 S_(n-1)的维度限制为 d × d,其信息存储容量存在上限。比如:如果原始上下文需要存储 20d² 的信息量,在压缩过程中将不可避免地损失 19d² 的信息。这揭示了线性注意力机制中计算效率与内存容量之间的根本性权衡:通过维持固定维度的状态矩阵获得计算效率的同时,也限制了上下文信息的保存能力。这一矛盾促使研究者们引入门控机制来优化这一权衡。
门控线性注意力机制
前文分析表明,在使用固定维度状态矩阵优化计算效率的过程中,信息损失是不可避免的。这引发了一个关键问题:是否可以通过某种机制来优化信息保留策略?门控机制正是为解决这一问题而提出的。研究者们将其作为一种选择性信息过滤机制,通过智能地选择需要保留的信息来最小化信息损失的影响。门控并非新概念,在 LSTM 等架构中已经得到了广泛应用和验证。
门控线性注意力对状态矩阵 Sn 的构建方式进行了改进:
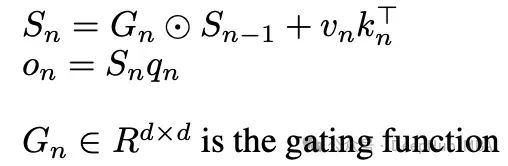
门控函数 G 有多种可能的实现方式,不同的选择会导致不同的模型特性:

来源:Yang, Songlin, et al. "Gated linear attention transformers with hardware-efficient training." _arXiv preprint arXiv:2312.06635_(2023).
这种架构的一个显著优势在于:门控函数仅依赖于当前 token x 和可学习参数,而不需要考虑完整的序列历史。由于各个 token 的门控计算相互独立,这种设计实现了训练过程的高效并行化,使得序列中所有 token 的门控运算能够同时进行。
状态空间模型
在处理序列数据(如文本或时间序列)时,传统方法通常依赖注意力机制或 RNN。状态空间模型(SSMs)提供了一种全新的视角:它将序列处理问题转化为类似于 CNN 处理图像的方式,通过卷积操作来捕获序列信息。
状态空间模型通过离散线性时不变系统来形式化这一思想:
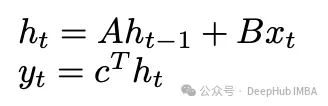
这种方法与卷积运算的关系可以表示为:

其中 F 表示从参数(A, B, c)学习得到的卷积核,*代表卷积运算。
H3 模型通过设计包含两个互补 SSM 层的结构化架构来实现这一理论框架:
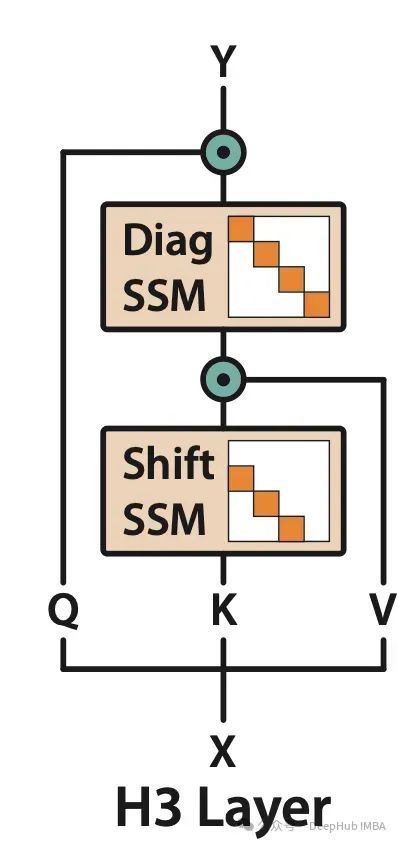
来源:Fu, Daniel Y., et al. "Hungry hungry hippos: Towards language modeling with state space models." arXiv preprint arXiv:2212.14052 (2022).
H3 将输入分解为三个通道以模拟 K、Q、V 结构,并通过组合两个 SSM 层和两个门控机制来模拟线性注意力的功能。实验结果表明,这种架构设计在实际应用中展现出了优异的性能。
选择性状态空间模型
前文讨论的门控线性注意力通过引入数据依赖的信息保留机制改进了标准线性注意力。状态空间模型同样面临类似的局限性:控制状态转换和输出的参数 A、B 和 c 都是固定且数据无关的。这意味着所有输入都要经过相同的静态系统处理,而不考虑输入的重要性或上下文信息。
为解决这一问题,研究者们提出了通过时变动力系统来扩展 SSMs:
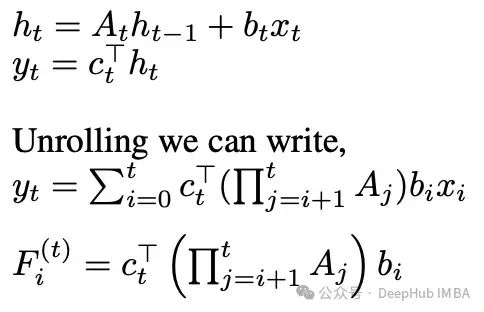
这种扩展的核心问题在于如何将 c_t、b_t 和 A_t 参数化为输入的函数。不同的参数化方案可能导致模型趋近于线性注意力或门控注意力机制。
Mamba 模型通过选择性 SSM 块实现了这种时变状态空间框架:
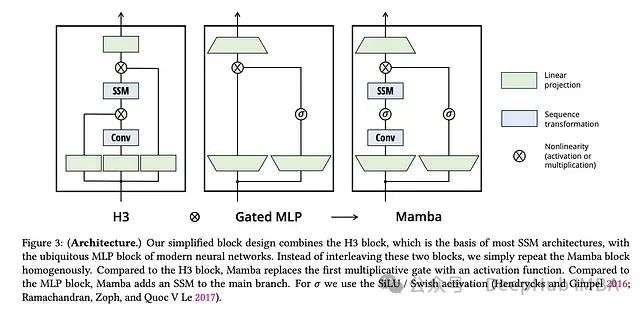
来源:Gu, Albert, and Tri Dao. "Mamba: Linear-time sequence modeling with selective state spaces." arXiv preprint arXiv:2312.00752 (2023).
Mamba 的创新之处在于用选择性 SSM 取代了标准 SSM,并结合输出门控和额外的卷积操作来提升性能。这种架构设计展示了如何将多个关键组件有机地整合为一个高效的序列建模系统。
总结
本文系统性地探讨了高效序列建模架构的演进历程。从传统 softmax 注意力机制的二次计算复杂度限制出发,研究者们发展出了线性注意力机制。通过核函数的重构,线性注意力实现了 O(Nd²)的计算复杂度,但同时也面临着固定维度状态矩阵带来的内存限制。
这一限制促使了门控线性注意力的提出,通过引入门控机制实现选择性信息保留。随后,状态空间模型提供了一个全新的视角,通过类卷积操作处理序列数据。从基础 SSMs 到时变系统,再到选择性 SSMs 的发展过程,与线性注意力到门控注意力的演进具有相似性——在这两个方向上,增强模型对输入数据的适应性都是提升性能的关键。
这些发展揭示了一个核心主题:计算效率与内存容量之间的基本权衡。softmax 注意力通过维持完整序列的注意力权重实现了出色的上下文学习能力,但付出了二次计算复杂度的代价。线性变体(包括 SSMs)通过固定维度的状态表示降低了计算复杂度,但也限制了保持详细上下文信息的能力。这种权衡仍然是序列建模领域的核心挑战,继续推动着研究者们探索能够更好平衡这些竞争需求的架构设计。
相关文献
线性注意力:Katharopoulos, Angelos, et al. "Transformers are rnns: Fast autoregressive transformers with linear attention." _International conference on machine learning_. PMLR, 2020.
GLA:Yang, Songlin, et al. "Gated linear attention transformers with hardware-efficient training." _arXiv preprint arXiv:2312.06635_(2023).
H3:Fu, Daniel Y., et al. "Hungry hungry hippos: Towards language modeling with state space models." arXiv preprint arXiv:2212.14052 (2022).
Mamba:Gu, Albert, and Tri Dao. "Mamba: Linear-time sequence modeling with selective state spaces." arXiv preprint arXiv:2312.00752 (2023).
Waleffe, Roger, et al. "An Empirical Study of Mamba-based Language Models." arXiv preprint arXiv:2406.07887 (2024).
https://avoid.overfit.cn/post/458a98aca6744a55af59ff65db2085e0



