神经网络技术已在计算机视觉与自然语言处理等多个领域实现了突破性进展。然而在微分方程求解领域,传统神经网络因其依赖大规模标记数据集的特性而表现出明显局限性。物理信息神经网络(Physics-Informed Neural Networks, PINN)通过将物理定律直接整合到学习过程中,有效弥补了这一不足,使其成为求解常微分方程(ODE)和偏微分方程(PDE)的高效工具。
传统神经网络模型需要依赖规模庞大的标记数据集,而这类数据的采集往往成本高昂且耗时显著。PINN 通过将物理定律(具体表现为微分方程)融入训练过程,显著提高了数据利用效率。这种方法使得在流体动力学、量子力学和气候系统建模等科学领域实现基于数据的科学发现成为可能,为跨学科研究提供了新的技术路径。
神经网络基础理论
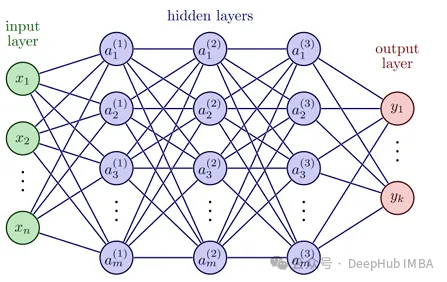
在深入剖析 PINN 之前,有必要回顾标准神经网络的核心运作机制:
神经网络的基本计算单元是神经元,它接收加权输入信号,经过激活函数处理后产生输出值。多层神经元通过特定拓扑结构组织形成深度神经网络(DNN),这种结构使网络能够逼近高度复杂的非线性函数。网络训练过程中,通常采用均方误差(MSE)等损失函数量化预测值与真实值之间的偏差。通过反向传播算法和梯度下降优化方法,网络权重参数被迭代调整以使损失函数最小化。
示例损失函数
均方误差
PINN 的技术特性与创新点
PINN 与传统神经网络的根本区别在于,它不依赖于标记数据集进行学习,而是将微分方程约束直接嵌入到损失函数中。这意味着模型学习得到的函数yNN(x)需同时满足:
- 给定的微分方程约束条件
- 特定的边界条件和初始条件
PINN 框架中的偏微分方程(PDE)通常表示为:
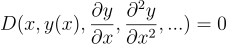
其中

以二阶微分方程为例:

这表明所求函数 y(x)必须严格满足该方程。
PINN 损失函数的构造原理
PINN 的总体损失函数由两个主要部分组成:

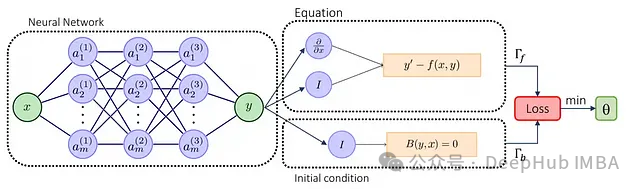
PINN 的技术优势与局限性
技术优势
PINN 具有显著的数据效率优势,能够通过物理定律的约束从相对小规模的数据集中有效学习。它能够处理传统数值求解器难以应对的高维复杂偏微分方程。训练完成后,PINN 模型具有良好的泛化能力,可预测不同初始条件或边界条件下的解。此外,在处理逆问题时,PINN 对噪声和稀疏数据表现出较强的鲁棒性。
技术局限
PINN 的训练过程计算密集且耗时较长,尤其对于高维偏微分方程,通常需要高性能 GPU 支持。模型对超参数选择较为敏感,需要精细调整以平衡不同损失项的贡献。与成熟的数值求解器相比,PINN 在处理大规模物理问题时可扩展性有限。此外,PINN 还面临梯度消失导致的优化困难问题,且缺乏与有限元或有限差分方法相当的理论收敛保证。
微分方程的解析求解方法
考虑以下一阶线性微分方程:
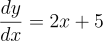
初始条件为:
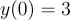
解法步骤
首先,将方程重写为标准形式:
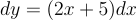
对方程两边进行积分:
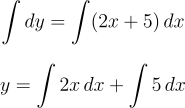
应用基本积分公式,得到 y 的表达式:
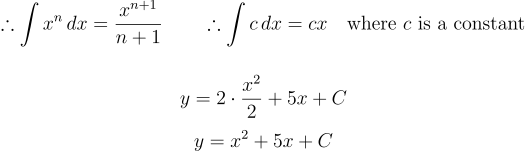
其中 C 为积分常数。
因此,通解为:
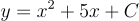
代入初始条件 y(0)=3: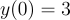
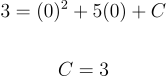
由此得到精确解:
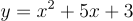
求解结果总结
通解形式:
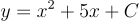
带入初始条件 y(0)=3 后的精确解:
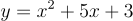
基于 PINN 求解微分方程的实践案例
步骤 1: 导入必要的库函数
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
from torchinfo import summary步骤 2: 定义能够返回精确解的函数
def true_solution(x):
return x**2 + 5*x + 3 ## 精确解函数这与我们手动求解得到的解析解一致
步骤 3: 生成测试点并绘制精确解
x_test = torch.linspace(-2, 2, 100).view(-1, 1) ## 生成测试点
y_true = true_solution(x_test)
plt.figure(figsize=(8, 5))
plt.plot( ## 绘制微分方程的精确解
x_test,
y_true,
linestyle="dashed" ,
linewidth=2,
label="True Solution"
)
plt.xlabel("x")
plt.ylabel("y(x)")
plt.legend()
plt.title("Analytical Solution of the Equation")
plt.grid()
plt.show()输出结果:
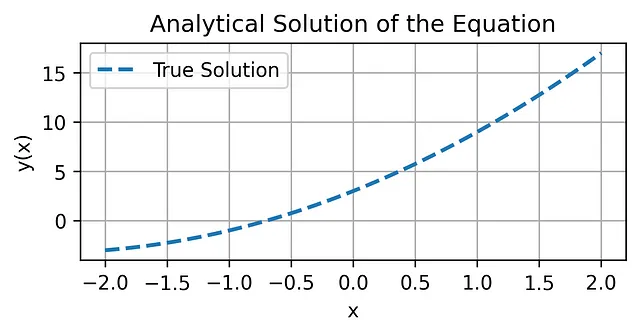
步骤 4: 设计 PINN 模型架构
class PINN(nn.Module):
def __init__(self):
super(PINN, self).__init__()
self.net = nn.Sequential(
nn.Linear(1, 20), nn.Tanh(),
nn.Linear(20, 20), nn.Tanh(),
nn.Linear(20, 1)
)
def forward(self, x):
return self.net(x)
model = PINN()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
summary(model)输出结果:

步骤 5: 定义 PINN 损失函数
def pinn_loss(model, x):
x.requires_grad = True
y = model(x)
## 使用自动微分计算dy/dx
dy_dx = torch.autograd.grad(y, x, torch.ones_like(y), create_graph=True)[0]
## 微分方程损失(L_D): dy/dx - (2x + 5)
ode_loss = torch.mean((dy_dx - (2*x + 5))**2)
## 初始条件损失(L_B): y(0) = 3
x0 = torch.tensor([[0.0]])
y0_pred = model(x0)
initial_loss = (y0_pred - 3)**2
## 总损失
total_loss = ode_loss + initial_loss
return total_loss, ode_loss, initial_loss步骤 6: 训练模型(5000 轮次)
epochs = 5000
loss_history = []
ode_loss_history = []
initial_loss_history = []
x_train = torch.linspace(-2, 2, 100).view(-1, 1) ## 训练点
for epoch in range(epochs):
optimizer.zero_grad()
total_loss, ode_loss, initial_loss = pinn_loss(model, x_train)
total_loss.backward()
optimizer.step()
loss_history.append(total_loss.item())
ode_loss_history.append(ode_loss.item())
initial_loss_history.append(initial_loss.item())
if epoch % 1000 == 0:
print(f"Epoch {epoch}, Loss: {total_loss.item():.6f}")步骤 7: 绘制训练过程中的损失函数变化
plt.figure(figsize=(8, 5))
epochs_list = np.arange(1, epochs + 1)
plt.semilogy(epochs_list, loss_history, 'k--', linewidth=3, label=r'Total Loss $(L_D + L_B)$')
plt.semilogy(epochs_list, ode_loss_history, 'r-', linewidth=1, label=r'ODE Loss $(L_D)$')
plt.semilogy(epochs_list, initial_loss_history, 'g-', linewidth=1, label=r'Initial Loss $(L_B)$')
plt.xlabel("Epochs")
plt.ylabel("Loss (Log Scale)")
plt.legend()
plt.title("Loss Components vs Epochs")
plt.grid()
plt.show()输出结果:
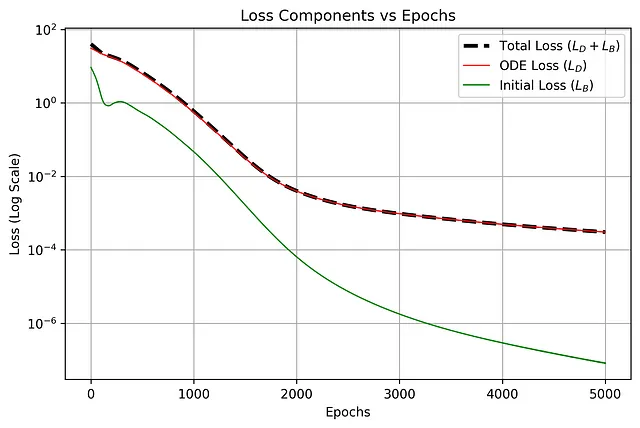
步骤 8: 对比 PINN 解与解析解的精确度
X_test = torch.linspace(-2, 2, 100).view(-1, 1)
y_pred = model(X_test).detach().numpy()
plt.plot(X_test,true_solution(X_test),linestyle="dashed",linewidth=3,label="True Solution",color="red")
plt.plot(X_test,y_pred,label="PINNS Solution",color="green")
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title(r'Analytical Vs PINNs Solution')
plt.savefig("solution.png", dpi=300, bbox_inches='tight')
plt.grid()
plt.show()输出结果:
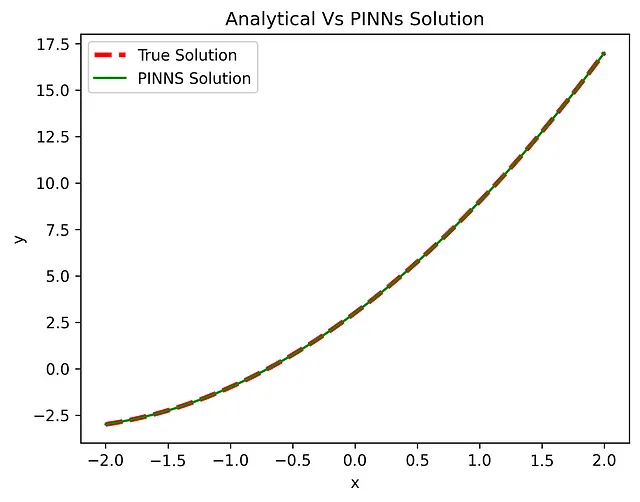
通过结果可以看出,我们已经成功地使用 PINN 方法求解了上述微分方程,并获得了与解析解高度一致的数值解。
总结
物理信息神经网络(PINN)代表了一种在微分方程求解领域的重要技术突破,它将深度学习与物理定律有机结合,为传统数值求解方法提供了一种高效、数据驱动的替代方案。PINN 方法不仅在理论上具有创新性,同时在实际应用中展现出广阔的应用前景,为复杂物理系统的建模与分析提供了新的研究路径。
https://avoid.overfit.cn/post/f9bd046772f1473a80002f592e9527d4



