本文从理论基础出发深入探讨图神经网络(Graph Neural Networks, GNNs)及以供应链需求预测为应用场景在多产品日销售量预测中的应用。在相关SKU构成的复杂网络中,单一产品的销售波动往往会对其他产品产生连锁影响。本文展示了如何通过学习稀疏影响图、应用图卷积融合邻居节点信息,并结合时间卷积捕获演化模式的完整技术路径,深入分析每个步骤的机制原理和数学基础。
传统时间序列预测方法如ARIMA或指数平滑通常将各产品视为独立个体进行处理,基于线性趋势假设,且要求数据满足平稳性条件或进行相应变换。当面对数十种产品间的相互作用关系,或需要整合促销活动、节假日效应、天气条件等外部信号时,这些方法往往力不从心。时间图神经网络通过学习产品关系的动态网络结构并捕获时间维度上的复杂模式,在统一的端到端模型框架内解决了这些挑战。读者不仅能够掌握实际应用技能,更将深入理解图邻接矩阵的数据驱动生成过程,以及时间卷积揭示隐含周期性规律的机制原理。
除供应链领域外,GNNs和时间GNNs在多个行业都有广泛应用前景:跨区域电力负荷预测、交通网络流量建模、电子商务产品推荐系统优化等。本文将重点介绍稀疏图正则化的创新技术,探讨不确定性估计的扩展方法,并提出后续研究方向,包括自适应图更新机制和实时重训练策略。
图神经网络与时间图神经网络基础理论
在众多预测任务中,特别是供应链中数十种产品销售量的预测场景,数据天然地形成图结构:每个产品作为图中的节点,边表示一个产品的历史销售对另一个产品销售的影响关系。图神经网络通过学习节点自身特征与邻居节点信息的融合表示,生成既考虑局部数据特性又尊重跨序列关系的嵌入向量。时间图神经网络在此基础上增加了时间维度的建模能力,通过专门的层结构捕获这些关系随时间演化的动态特性。
图神经网络架构设计
图神经网络将数据建模为图G = (V, E),其中每个节点v_i承载特征向量x_i(如前日销售量、库存水平等属性),每条边(i, j)具有学习得到的权重a_{ij},表示节点j对节点i的影响强度。
核心目标是为每个节点计算隐藏状态h_i,该状态有效融合了节点自身特征和来自邻居节点的信息传递。
消息传递神经网络的数学框架
消息传递神经网络(Message Passing Neural Networks, MPNNs)构成了大多数GNN架构的理论基础,在预测模型中发挥核心作用。MPNNs的计算过程包含两个关键步骤:首先是消息计算,每个节点从其邻居节点j接收消息m{ij};其次是聚合更新,将所有传入消息与节点自身特征结合,通过小型多层感知器(MLP)处理生成新的节点表示h'i。
在第k层的形式化表达为: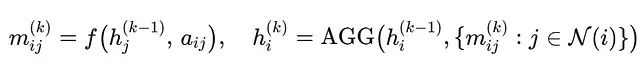
其中f表示简单的线性变换或注意力函数,AGG可以选择均值池化、加权求和或注意力机制。经过K层处理后,如果需要图级别的表示,可通过读出步骤(如对所有h_i^(K)求和或平均)获得图级向量。
GNN层的计算流程可以表示为:
输入到第k层: h_i(k-1) ← 前一层的节点嵌入向量
│
边消息计算: m_ij = f(h_i, h_j, a_ij)
│
邻居信息聚合: Σ_j m_ij (或均值/最大值池化)
│
节点状态更新: h_i(k) = MLP([h_i(k-1) || aggregated])与多层感知器的架构对比分析
MPNNs与多层感知器在计算原理上具有相似性,都执行线性变换后接非线性激活的操作,本质上都可以视为"具有特定结构的隐藏层"。关键差异在于连接拓扑结构和参数共享机制:
输入 = 节点特征 + 邻接关系信息
输出 = 更新后的节点特征向量与传统MLP的核心区别在于:标准MLP中隐藏层采用全连接架构,权重参数仅由层索引确定;而在MPNNs中,连接模式由图的邻接结构控制,权重参数基于图结构进行学习。
从卷积神经网络到图卷积网络的理论扩展
图神经网络,特别是图卷积网络(Graph Convolutional Networks, GCNs),将卷积操作扩展到非欧几里得结构数据。最初为分子性质预测和计算机视觉任务开发,GNNs将原子视为分子中的节点,化学键作为边,或将像素区域及其在不规则图像数据中的关系(如超像素、3D网格)进行建模。
传统CNNs在固定邻域(如3×3网格)上应用卷积核,假设平移等变性;而GCNs在图G=(V, E)上操作,每个节点v_i可能具有可变数量的邻居节点。卷积操作转换为消息传递机制:节点从其邻居收集并转换信息。
GCN层的数学定义为: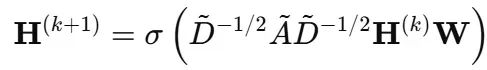
其中A=A+I添加自环连接,D为度矩阵,W为共享权重矩阵。
这种设计使得GCNs具有以下优势:在边上共享权重实现参数效率,逐层捕获局部结构(每层处理1-hop邻域),使用邻接归一化稳定训练过程,并且具有置换等变性,使其成为图结构数据学习的理想选择。
注意力机制在图神经网络中的重要性
图注意力网络(Graph Attention Networks, GATs)将注意力机制引入GNNs,解决了一个关键问题:并非所有邻居节点都具有相同的重要性。在标准GCNs中,来自所有邻居的消息被平均处理或按度数加权,这在某些邻居节点不相关或度数差异较大的图中可能引入噪声。
GATs通过学习注意力权重α_{uv}来解决这一问题,该权重衡量邻居节点v对节点u的重要程度。这些权重从节点特征计算得出,而非从图结构推导,使得模型能够学习识别重要邻居,而不是将所有边视为等价。
数学表达式为: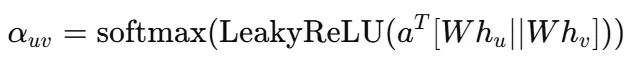
其中a和W为可学习参数,softmax确保节点周围所有权重之和为1。因此节点从邻居收集消息时,对有用邻居赋予更高权重。
通常采用多头注意力机制,即网络计算多个注意力分数α并将其组合。这有助于降低噪声并捕获数据中不同类型的模式。
注意力机制的另一个优势是可解释性。注意力分数显示哪些节点对输出产生影响,对于产品推荐或预测等任务,了解"原因"同样重要。
稀疏性在图神经网络中的作用机制
稀疏GNNs专门设计用于处理大规模图数据,通过仅关注最重要的连接来提高效率。与使用每条边不同,这些方法在训练过程中应用L1正则化、top-k剪枝或边采样等技术移除弱连接,从而减少内存使用并加速计算。
通过向损失函数添加λ‖A‖₁等项,模型学习稀疏的邻接矩阵或注意力矩阵,其中许多权重收缩至零,使得结构既高效又更具可解释性。
稀疏GNNs特别适合处理天然稀疏的现实世界网络,如社交图谱或产品推荐系统,其中大多数节点仅具有少数强连接。更少、更清晰的连接也有助于解释模型决策,使得更容易追踪"SKU-7 → SKU-10"等影响路径。
图神经网络的端到端训练策略
标准GNN通过最小化组合损失函数进行训练: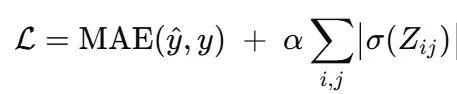
其中Z ∈ R^{N×N}为邻接logits矩阵,a{ij} = σ(Z{ij})为学习得到的边权重。L₁惩罚项将大多数a_{ij}推向零,产生稀疏且可解释的图结构。
训练步骤详述
输入特征为X ∈ R^{N×F},其中N个节点中的每一个都具有F个特征(如产品属性或历史销售数据)。
图卷积操作基于邻居关系和当前邻接矩阵A更新节点嵌入。在每层后使用ReLU激活函数引入非线性;堆叠K层以捕获最多K-hop的结构信息。
优化器采用学习率为3×10^{-4}的AdamW。正则化包括对σ(Z)的L₁惩罚以剪枝弱边并强制稀疏性。
监控验证集上的平均绝对误差(MAE)进行早停,确保模型具有良好的泛化能力而不会过拟合。
时间图神经网络架构
时间GNN为标准GNN增加了时间维度建模能力,捕获关系随时间演化的动态特性。
整体流程可以表示为:
时间 t-2 时间 t-1 时间 t
┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐
│ GNN层 │ │ GNN层 │ │ GNN层 │
│ (空间处理) │ │ (空间处理) │ │ (空间处理) │
└────────┬────────┘ └────────┬────────┘ └────────┬────────┘
│ │ │
产品 1 ──● x₁,t-2 ─────────────▶● x₁,t-1 ─────────────▶ ● x₁,t
│ │ │
│ │ │
产品 2 ──● x₂,t-2 ─────────────▶● x₂,t-1 ─────────────▶ ● x₂,t
│ │ │
│ │ │
产品 N ──● x_N,t-2─────────────▶● x_N,t-1─────────────▶ ● x_N,t
│ │ │
▼ ▼ ▼
(通过学习图A (通过相同图A (通过相同图A
传递消息) 传递消息) 传递消息)
──────────────────────── 时间卷积 / 循环神经网络 ───────────────────────▶
(扩张Conv1d捕获滞后效应、季节性)
▼
时间维度池化操作
▼
线性投影层 → 7天预测结果
▼
输出张量 (batch, horizon, N)时间GNN(TGNN)基于GNN的空间(图)结构建模能力,通过添加时间卷积网络(TCN)来捕获序列模式。在学习图结构A后,在每个时间步应用图卷积,然后将节点嵌入序列输入扩张1D卷积: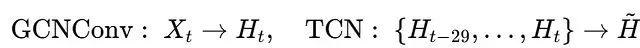
其中TCN使用核大小3和扩张因子2来捕获长距离依赖关系。最终的线性层将H~投影到每个产品的7天预测结果。
时间GNN的详细实现与训练
以下代码展示了时间图学习器的工作原理:
# ──────────────────────────────────────────────────────────────────
# 1. ⓖ 图学习器 → 每步生成(软)邻接矩阵 A_t
# ──────────────────────────────────────────────────────────────────
class GraphLearner(nn.Module):
def forward(self, X_t): # X_t: [N, F]
# 相似性计算/稀疏化处理;具体实现细节省略
A_t = ... # [N, N] 行随机化
return A_t
# ──────────────────────────────────────────────────────────────────
# 2. ⓢ 空间编码器 (GCN / GAT / 任意消息传递算子)
# ──────────────────────────────────────────────────────────────────
class SpatialEncoder(nn.Module):
def forward(self, X_t, A_t): # 返回 H_t: [N, H]
H_t = ... # GNN层 + ReLU激活
return H_t
# ──────────────────────────────────────────────────────────────────
# 3. ⓣ 时间编码器 (TCN / GRU / Transformer编码器等)
# ──────────────────────────────────────────────────────────────────
class TemporalEncoder(nn.Module):
def forward(self, H_seq): # H_seq: [B, N, H, T]
Z = ... # 1-D 卷积 / 扩张操作
return Z # [B, H]
# ──────────────────────────────────────────────────────────────────
# 4. 主模型架构 – 整合 ⓖ ⓢ ⓣ → 预测期预测
# ──────────────────────────────────────────────────────────────────
class TemporalGNN(nn.Module):
def __init__(self, in_dim, hid_dim, horizon):
super().__init__()
self.glearner = GraphLearner()
self.spatial = SpatialEncoder()
self.temporal = TemporalEncoder()
self.head = nn.Linear(hid_dim, horizon)
def forward(self, X): # X: [B, N, F, T]
H_stack, l1_reg = [], 0.0
for t in range(X.size(-1)):
X_t = X[..., t] # 时间步切片
A_t = self.glearner(X_t) # 学习/更新图结构
H_t = self.spatial(X_t, A_t) # 空间信息融合
H_stack.append(H_t)
l1_reg += A_t.abs().mean() # 稀疏性正则化项
H_seq = torch.stack(H_stack, dim=-1) # [B, N, H, T]
Z = self.temporal(H_seq) # 时间信息融合
ŷ = self.head(Z) # [B, horizon]
return ŷ, l1_reg
# ──────────────────────────────────────────────────────────────────
# 5. 训练循环(伪代码)– MAE + λ·L¹(A) , AdamW, 早停
# ──────────────────────────────────────────────────────────────────
def train(model, dataloader):
for batch in dataloader:
ŷ, l1 = model(batch.x)
loss = MAE(ŷ, batch.y) + λ * l1
...
# ──────────────────────────────────────────────────────────────────
# 6. 预测结果:调用 model(batch.x)[0] → 未来k天销售向量
# ──────────────────────────────────────────────────────────────────模型架构与优化策略
模型架构以GCNConv(in_channels, hidden)开始,使用学习得到的邻接矩阵A融合节点特征,应用ReLU激活,并将输出重塑为(batch, hidden, time)格式。Conv1d层采用kernel_size=3, dilation=2, padding=2的配置捕获时间模式,结果经时间维度平均后通过Linear(hidden, horizon)头部进行多步预测。
训练过程使用AdamW优化器联合优化GCN、TCN和稀疏图参数,添加L₁惩罚鼓励图稀疏性。基于验证MAE的早停策略确保泛化能力并防止过拟合。
时间图神经网络在多变量销售趋势预测中的应用
在前一节中,我们阐述了图神经网络的核心原理,重点介绍了时间GNNs的理论基础、训练过程和整体工作流程。本节将这些理论概念应用到具体的业务场景中,展示时间GNNs如何通过多变量销售趋势建模实现供应链需求预测。
考虑一个典型场景:五十个SKU共享同一仓库货架空间。第7项产品今日的折扣促销可能会转移第10项产品明日的需求;周末效应或节假日激增驱动所有序列同步变化;然而每个SKU仍保持其独特的季节性特征。
观察数据矩阵: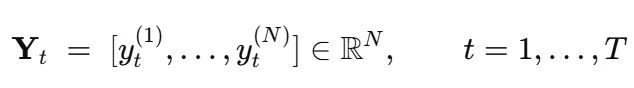
目标是预测每行的未来7个数据点。经典的单变量ARIMA方法忽略跨SKU渗透效应;纯RNN方法将所有信息展平处理,丢失了"谁影响谁"的结构信息。本文方法结合两个互补概念:
稀疏图学习器推断有向加权图A,指示哪个产品引导或滞后于其他产品;时间GNN模块每日运行图卷积,然后执行捕获短期和中期季节性的时间卷积(扩张1×3核)。
两者共同构成预测函数: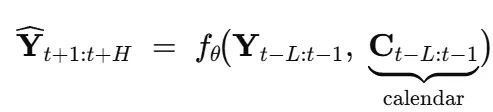
其中L = 30表示输入网络的历史天数,H = 7表示预测天数,θ代表所有可学习权重(图结构、GCN、TCN、线性头)。
数据预处理:从不规则零售日志到学习就绪张量
日历特征编码通过sin(2π DOY/365)、cos(2π DOY/365)和工作日整数为网络提供周/年节律信息,帮助模型理解常规需求模式。
列级标准化每个SKU具有独特的均值和方差,因此采用独立的z-score标准化: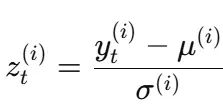
这种处理防止高销量SKU在损失函数中占主导地位。
滑动窗口构建每个训练样本为张量: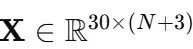
目标为下一时段的7天切片,但仅包含销售部分(3个外生日历列不参与预测)。
稀疏影响图的学习机制
学习器维护无约束logits矩阵Z ∈ R^{N×N}。通过sigmoid函数映射到[0,1]区间的概率: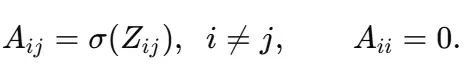
图在初始时刻是密集的,但通过添加L₁惩罚: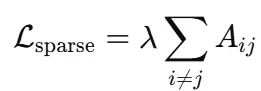
在梯度下降过程中将弱边推向零。效果是发现仅有少数真实交互关系(例如"SKU-7 ⟶ SKU-10")。
由于A在每次前向传播中重新计算,网络可以在学习时间权重的同时适应拓扑结构,实现端到端的图结构学习。
空间和时间维度的消息传递机制
每日图卷积处理
对30天窗口中的每一天,创建节点特征向量h_d^(i)并展平批次处理。单个GCN层更新节点状态: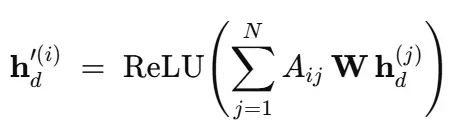
其中: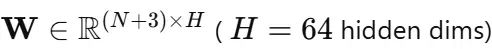
直观理解:每个SKU使用与A_{ij}成比例的学习权重从其影响者混合信息。
时间卷积处理
将更新后的30×64矩阵堆叠成形状(H, 30)并输入扩张1-D卷积核: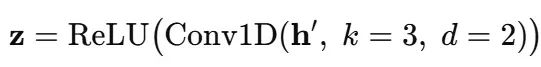
扩张意味着卷积核同时观察滞后0, 2, 4的时间点;堆叠扩张因子(2, 4, 8, …)使网络能够在无需深度递归的情况下捕获月度节律。
最终,沿30天轴进行均值池化;输出向量z ∈ R^H是最近图感知动态的紧凑、序列不变摘要。
多步预测的线性投影
全连接层将z映射到H = 7个标量: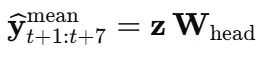
由于损失函数对真实50-SKU张量进行平均,ŷ表示所有SKU的预期7天平均销售,这是许多规划师关注的聚合关键绩效指标。(当然,也可以预测完整的7×N立方体;只需保留最后的张量维度而不是在SKU上池化。)
目标函数与优化策略
网络最小化以下损失函数: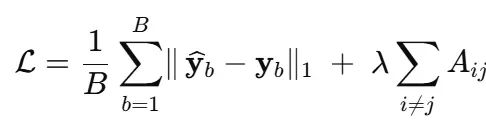
MAE (L1)损失保持预测中位数对齐并对异常值稳健;L₁图惩罚强制稀疏性,使小相关性被修剪。
采用学习率为3×10^-4的AdamW优化器处理密集权重和稀疏logits。每个epoch的运行流程:
前向传播 → 计算A、GCN消息、TCN、损失;反向传播 → 梯度通过图结构传播(因为A是可微的)。
防止信息泄漏的时间分割策略
滑动窗口按时间顺序分割:前70%用于训练,接下来15%用于验证,最后15%用于测试。这种分割反映现实世界预测场景,其中未来需求不能访问后续时间的数据。基于验证MAE的早停策略冻结最佳检查点。
逆标准化与模型评估
预测时使用以下公式撤销全局z-score标准化: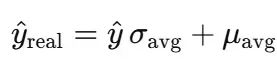
然后计算MAPE: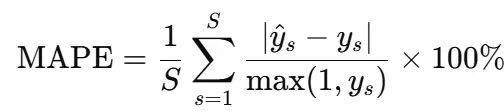
使用全局均值/标准差(而非每个SKU独立)与"所有SKU平均"目标一致,因此度量真正反映对联合组合的百分比误差。
基线方法:跨序列数据的SARIMAX与SES比较
经典基线方法逐个预测每个SKU:
SARIMAX(1,0,1)处理自回归和移动平均特性,但没有直接通道处理产品间效应。当SKU-7影响SKU-10时,SARIMAX必须依赖lag-7自回归项作为代理。简单指数平滑假设需求遵循带漂移均值的随机游走,适合平稳的日用品但会迅速错过协调的促销激增。
相比之下,TGNN通过学习的邻接矩阵直接注入其他SKU的信号,当第7项的促销标志激活时,边A_{7,10}将激增传播到第10项的节点向量,TCN立即观察到这种影响。
代码实验与结果分析
本节专注于供应链任务:预测多个相关产品的销售以支持规划、库存控制和补货决策。准确的短期预测有助于避免缺货并减少过量库存。数据集包含50个SKU的日销售数据,以及工作日和季节性等日历特征(通过年中日的正弦/余弦表示)。这些特征帮助模型捕获常规需求模式。核心挑战是建模跨SKU影响关系,其中一个产品的促销可能影响另一个产品,这正是时间GNN展现优势的场景。
完整的实现代码如下:
import pandas as pd, numpy as np, torch, torch.nn as nn
from sklearn.preprocessing import StandardScaler
# 1) 数据加载 ───────────────────────────────
output_csv_path = "aggregated_sales.csv"
df = pd.read_csv(output_csv_path, parse_dates=["date"]).set_index("date")
# 数据形状: (T, N) 例如 (800, 50)
# 2) 添加日历协变量 (sin/cos, weekday)
cal = pd.DataFrame({
"sin_doy": np.sin(2*np.pi*df.index.dayofyear/365),
"cos_doy": np.cos(2*np.pi*df.index.dayofyear/365),
"weekday": df.index.weekday
}, index=df.index)
full = pd.concat([df, cal], axis=1)
# 3) 分别标准化每列
scaler = StandardScaler()
X = scaler.fit_transform(full)
X = torch.tensor(X, dtype=torch.float32) # (T, N + 3)
# 4) 滑动窗口数据集构建
HIST, HORIZON = 30, 7 # 历史30天 → 预测7天 (可调整)
seq, tgt = [], []
for t in range(HIST, len(X) - HORIZON + 1):
seq.append(X[t-HIST:t]) # (30, N+3)
tgt.append(X[t:t+HORIZON, :df.shape[1]]) # 仅销售部分作为目标
seq = torch.stack(seq) # (samples, 30, D)
tgt = torch.stack(tgt) # (samples, 7, N)
class SparseGraphLearner(nn.Module):
def __init__(self, n_nodes, l1_alpha=1e-3):
super().__init__()
self.A_logits = nn.Parameter(torch.randn(n_nodes, n_nodes))
self.l1 = l1_alpha # 稀疏性权重
def forward(self):
A = torch.sigmoid(self.A_logits) # (0,1)
A = A * (1 - torch.eye(A.size(0))) # 移除自环
return A
def l1_loss(self):
return self.l1 * torch.abs(torch.sigmoid(self.A_logits)).sum()
##############
from torch_geometric.nn import GCNConv
class TGNN(nn.Module):
def __init__(self, n_series, hidden=64, horizon=HORIZON):
super().__init__()
self.glearner = SparseGraphLearner(n_series)
self.gc1 = GCNConv(in_channels=n_series+3, out_channels=hidden)
self.tcn = nn.Conv1d(hidden, hidden, kernel_size=3, dilation=2, padding=2)
self.head = nn.Linear(hidden, horizon) # 每个节点的多步预测
def forward(self, seq): # seq: (B, L, D) 其中 D=N+3
A = self.glearner() # (N,N)
edge_index = A.nonzero().t() # COO格式索引
edge_weight = A[edge_index[0], edge_index[1]]
# 为图卷积重塑:分别处理每个时间步
B, L, D = seq.shape
x = seq.reshape(B*L, D) # 节点=batch*L
x = self.gc1(x, edge_index, edge_weight)
x = torch.relu(x).reshape(B, L, -1).permute(0,2,1) # (B, hidden, L)
h = torch.relu(self.tcn(x)) # 时间特征提取
h = torch.mean(h, dim=-1) # (B, hidden)
out = self.head(h) # (B, horizon)
return out, A
###########################################################
# 训练循环 (设备无关:CPU或GPU都支持) #
###########################################################
# ──────────────────────────────────────────────────────────
# 将seq / tgt时间序列样本按时间序分割为训练 / 验证 / 测试
# - 时间顺序分割以避免数据泄漏
# ──────────────────────────────────────────────────────────
TOTAL = len(seq)
train_end = int(0.7 * TOTAL) # 70%训练
val_end = int(0.85 * TOTAL) # 15%验证,15%测试
seq_train, tgt_train = seq[:train_end], tgt[:train_end]
seq_val, tgt_val = seq[train_end:val_end], tgt[train_end:val_end]
seq_test, tgt_test = seq[val_end:], tgt[val_end:]
print(f"训练:{len(seq_train)}, 验证:{len(seq_val)}, 测试:{len(seq_test)}")
# ──────────────────────────────────────────────────────────
# 设备配置 + 训练循环
# ──────────────────────────────────────────────────────────
import torch, torch.nn as nn
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(">> 在以下设备上训练:", DEVICE)
model = TGNN(n_series=df.shape[1]).to(DEVICE)
opt = torch.optim.AdamW(model.parameters(), lr=3e-4)
loss_fn = nn.L1Loss() # 标准化空间中的MAE
BATCH = 64
def batch_iter(x, y, bs):
idx = torch.randperm(len(x))
for i in range(0, len(x), bs):
j = idx[i:i+bs]
yield x[j].to(DEVICE), y[j].to(DEVICE)
for epoch in range(80):
# ---- 训练阶段 ----
model.train(); train_mae = 0.0
for xb, yb in batch_iter(seq_train, tgt_train, BATCH):
opt.zero_grad()
pred, _ = model(xb)
loss = loss_fn(pred, yb.mean(-1)) + model.glearner.l1_loss()
loss.backward(); opt.step()
train_mae += loss_fn(pred, yb.mean(-1)).item() * len(xb)
# ---- 验证阶段 ----
model.eval(); val_mae = 0.0
with torch.no_grad():
for xb, yb in batch_iter(seq_val, tgt_val, BATCH):
pred, _ = model(xb)
val_mae += loss_fn(pred, yb.mean(-1)).item() * len(xb)
train_mae /= len(seq_train)
val_mae /= len(seq_val)
print(f"E{epoch:02d} train-MAE {train_mae:.4f} | val-MAE {val_mae:.4f}")
#########
# ───────────────────────────────
# 1) 计算整体平均标准化因子(单一标量)
# ───────────────────────────────
avg_scale = torch.tensor(scaler.scale_[:df.shape[1]].mean(), dtype=torch.float32)
avg_mean = torch.tensor(scaler.mean_ [:df.shape[1]].mean(), dtype=torch.float32)
# ───────────────────────────────
# 2) 预测与逆变换
# ───────────────────────────────
model.eval(); preds, trues = [], []
with torch.no_grad():
for xb, yb in batch_iter(seq_test, tgt_test, BATCH):
p, _ = model(xb.to(DEVICE))
preds.append(p.cpu())
trues.append(yb.mean(-1).cpu()) # 与训练一致
preds = torch.cat(preds) * avg_scale + avg_mean # (samples, horizon)
trues = torch.cat(trues) * avg_scale + avg_mean
# ───────────────────────────────
# 3) 计算out-of-time MAPE
# ───────────────────────────────
mape = ((preds - trues).abs() / trues.clamp(min=1e-8)).mean().item() * 100
print(f"Out-of-time MAPE = {mape:.2f} %")
A = model.glearner().cpu().detach().numpy()
import networkx as nx, matplotlib.pyplot as plt
G = nx.from_numpy_array(A, create_using=nx.DiGraph)
# 设置可视化阈值
G = nx.DiGraph( (u,v,d) for u,v,d in G.edges(data=True) if d['weight']>0.15 )
nx.draw(G, node_size=300, arrows=True)
# =========================================================
# 5. 经典基线:SARIMAX和SES比较
# =========================================================
# -----------------------------------------------------------
# 通用一步前向滚动预测器 (适用于两种方法)
# -----------------------------------------------------------
def rolling_forecast(model_builder, history, steps, fit_kwargs=None):
fit_kwargs = fit_kwargs or {}
hist = list(history)
out = []
for _ in range(steps):
model = model_builder(hist) # 构建新模型
result = model.fit(**fit_kwargs)
fc = result.forecast(1)[0]
out.append(fc)
hist.append(fc) # 滚动窗口更新
return np.array(out)
test_len = len(seq_test) # 滚动步数
train_raw = df.iloc[:val_end + HIST] # 数据到测试开始
sarimax_preds, ses_preds = [], []
for col in df.columns:
trn = train_raw[col].values
# SARIMAX(1,0,1)
sarimax_preds.append(
rolling_forecast(
lambda h: SARIMAX(h, order=(1,0,1)),
trn, test_len,
fit_kwargs={"disp": False}
)
)
# 简单指数平滑
ses_preds.append(
rolling_forecast(
lambda h: SimpleExpSmoothing(h, initialization_method="estimated"),
trn, test_len
)
)
sarimax_preds = np.column_stack(sarimax_preds).mean(axis=1) # 对齐形状
ses_preds = np.column_stack(ses_preds).mean(axis=1)
# ---------- MAPE辅助函数 ----------
def mape(pred, true):
return np.mean(np.abs(pred-true) / np.clip(true, 1e-8, None)) * 100
truth_avg = trues.mean(axis=1) # (samples,)
sx_mape = mape(sarimax_preds, truth_avg)
ses_mape = mape(ses_preds, truth_avg)
print("\n============= OUT-OF-TIME MAPE =============")
print(f"SARIMAX(1,0,1) : {sx_mape:6.2f} %")
print(f"SES : {ses_mape:6.2f} %")仅用几百行PyTorch/torch-geometric代码,该流水线在50序列零售数据集上实现个位数百分比误差,同时揭示产品间影响关系,为需求规划师和寻求透明、可更新模型的数据科学家提供了宝贵价值。
实验结果如下:
E73 train-MAE 0.3244 | val-MAE 0.4051
E74 train-MAE 0.3217 | val-MAE 0.4113
E75 train-MAE 0.3239 | val-MAE 0.4256
E76 train-MAE 0.3252 | val-MAE 0.3988
E77 train-MAE 0.3225 | val-MAE 0.4143
E78 train-MAE 0.3203 | val-MAE 0.3994
E79 train-MAE 0.3159 | val-MAE 0.4021
Out-of-time MAPE = 9.70%
SARIMAX(1,0,1) : 20.69%
SES : 18.73%训练过程的最后几个epoch显示训练和验证MAE(平均绝对误差)保持稳定,表明时间GNN已学习到有意义的模式而未出现过拟合。验证MAE维持在0.40左右,表明模型对未见数据具有良好的泛化能力。
Out-of-time MAPE(平均绝对百分比误差)为9.70%,意味着模型在真实未来销售预测上的平均误差低于10%,这对多变量预测而言是一个优秀的结果。
与传统模型的对比中,SARIMAX和SES分别显示出更高的误差(20.69%和18.73%)。这凸显了时间GNN在捕获供应链需求中产品依赖关系和时间模式方面的优越性。
总结
本文深入探讨了时间图神经网络(TGNNs)在供应链环境中预测多产品需求的应用。我们详细分析了空间组件(GNN)如何学习产品间相互影响关系,以及时间组件(TCN)如何捕获季节性和趋势特征。通过将两者有机结合,构建了一个统一模型,能够读取批量时间序列并一次性输出30天需求预测,无需处理单独的产品预测器。
在实际应用中,这种TGNN可以在促销活动、节假日标志和库存水平等特征上进行训练。训练完成后,它为规划师提供了深入洞察,例如"产品A在周末的激增会带动产品B的销售"或"促销活动在黑色星期五前一周推动需求增长"。当需要平衡库存、仓库容量和营销预算时,这种洞察具有重要价值,所有信息都集成在单一仪表板中。
TGNNs在任何具有相关时间序列网络的场景中都表现出色:城市区域间的交通流量、互联电网中的能源消耗,或医院病房中的患者生命体征监测。它们通过原生处理非线性跨序列效应并整合外部信号(促销、事件)而无需额外特征工程,超越了经典工具的性能。
建议不要局限于点预测。可以加入Monte Carlo dropout或简单模型集成来量化不确定性(例如"SKU123的需求有80%的概率保持在1,000–1,200单位范围内")。这样,不仅能知道可能发生什么,还能了解预测的置信度。对于任何在动态条件下追求多产品预测的团队,TGNNs提供了实用的端到端解决方案。
完整代码和数据集可在以下地址获取:
https://avoid.overfit.cn/post/6c7dbc14da2e423eae4764559f6bf8e2



