考虑这样一个实际场景:在构建用于预测200家医院患者住院时长的模型时,尽管梯度提升模型在测试集上表现优异,但深入分析会发现一个系统性问题:医院A的住院时长始终高于模型预测值,而医院B则总是低于预测值。传统模型对所有医院采用相同的预测策略,忽略了各医院间的系统性差异,从而错失了提升预测准确性和获得更深入洞察的机会。
混合效应模型正是解决此类问题的有效工具,深入理解其实现机制将为数据科学家提供重要的技术优势。
混合效应模型的核心价值
在深入技术细节之前,需要明确混合效应模型在现代机器学习生态系统中的独特价值和应用意义。
混合效应模型相对于标准机器学习方法的优势
在深度学习和集成方法广泛应用的背景下,一个自然的疑问是:为什么不直接将医院ID作为特征输入XGBoost等算法?
关键问题在于标准机器学习方法处理分组数据时面临的两难选择:固定效应方法将每个医院视为独立的分类特征,这会导致稀疏矩阵问题和过拟合风险;无效应方法则完全忽略医院间的差异,丢失了重要的系统性模式信息。
混合效应模型提供了第三种解决方案:通过学习收缩机制,自动确定每个组相对于总体平均水平的偏离程度,在个体组特性和全局趋势之间实现最优平衡。这种方法不仅在统计学上更为严谨,在计算效率和结果可解释性方面也具有显著优势。
自主实现的必要性分析
尽管R语言的lme4包、SAS的PROC MIXED过程以及Python的statsmodels库都提供了成熟的混合效应模型实现,但在某些场景下自主实现仍具有重要意义。
算法定制需求:当面对特定领域的专业要求时,标准库往往无法满足定制化需求。例如,根据领域专业知识修改收敛准则、将混合效应机制集成到神经网络架构中、为时间序列或空间数据实现非标准协方差结构、与现代机器学习管道中的特殊数据格式进行集成等。
创新研究驱动:理解算法内部机制能够促进技术创新,包括将收缩概念嵌入transformer注意力机制、构建平衡个体和组级目标的混合损失函数、开发支持实时组效应更新的流式算法、构建基于方差分解的可解释AI系统等。
生产环境优化:生产级机器学习系统通常需要进行算法层面的优化,这包括针对大规模分组数据的稀疏矩阵操作优化、GPU加速实现以支持深度学习集成、内存高效算法以适应边缘部署场景、以及针对特定领域的数值稳定性改进等。
实现知识的价值不在于替代现有工具,而在于当创新需求超越现有工具限制时提供技术突破的可能性。
数学基础与核心原理
混合效应模型的核心思想在于将预测结果分解为固定效应和随机效应两个组成部分: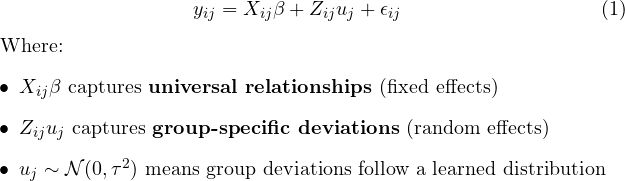
以本文的例子为背景,如果患者年龄与住院时长之间存在每年0.3天的普遍关联,这构成固定效应;而某医院由于保守的出院政策导致的系统性2天延长,则属于随机效应范畴。
模型的关键创新在于随机效应的分布假设。与将每个组独立处理的虚拟变量方法不同,混合效应模型假设组偏差来自共同的概率分布。这一假设实现了自动正则化和跨组信息共享机制,为特定机器学习应用的定制化开发提供了强大的理论基础。
潜在变量估计挑战
混合效应模型实现的核心难点在于随机效应u作为潜在变量的特性,它们在概念上存在但无法直接观测。这导致了一个相互依赖的估计问题:固定效应β的估计需要已知随机效应u,而随机效应u的估计又依赖于固定效应β。
传统机器学习方法不会遇到这种挑战,因为所有特征都是可观测的。混合效应模型必须采用在这些相互依赖组件估计之间交替迭代的算法策略。
期望最大化算法实现
以下将逐步构建完整的混合效应模型实现,展示标准库隐藏的算法细节。
基础框架构建
import numpy as np
from scipy.optimize import minimize
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import seaborn as sns
class MixedEffectsFromScratch:
def __init__(self, groups):
"""使用组结构初始化模型"""
self.groups = np.array(groups)
self.unique_groups = np.unique(groups)
self.n_groups = len(self.unique_groups)
# 预计算组索引以提高计算效率
self.group_indices = {
g: np.where(groups == g)[0]
for g in self.unique_groups
}
def _initialize_parameters(self, y, X):
"""基于OLS的智能参数初始化"""
# 使用总体水平估计作为起始点
ols_model = LinearRegression(fit_intercept=False)
ols_model.fit(X, y)
self.beta = ols_model.coef_
residual_var = np.var(y - X @ self.beta)
# 合理分配组内和组间方差组件
self.sigma2 = residual_var * 0.7 # 组内方差
self.tau2 = residual_var * 0.3 # 组间方差参数初始化策略对算法收敛性至关重要。通过OLS获得合理的固定效应初始值,通过分割残差方差为方差组件提供适当的起始估计。
E步实现:收缩机制的核心
E步通过最佳线性无偏预测器(BLUPs)估计随机效应,这是收缩现象的实现关键:
def _e_step(self, y, X):
"""通过收缩公式估计随机效应"""
residuals = y - X @ self.beta
random_effects = np.zeros(self.n_groups)
for i, group in enumerate(self.unique_groups):
group_idx = self.group_indices[group]
group_residuals = residuals[group_idx]
n_j = len(group_idx)
# 收缩公式——混合效应模型的核心机制
shrinkage_factor = self.tau2 / (self.tau2 + self.sigma2 / n_j)
random_effects[i] = shrinkage_factor * np.mean(group_residuals)
return random_effects收缩公式的深层含义值得特别关注: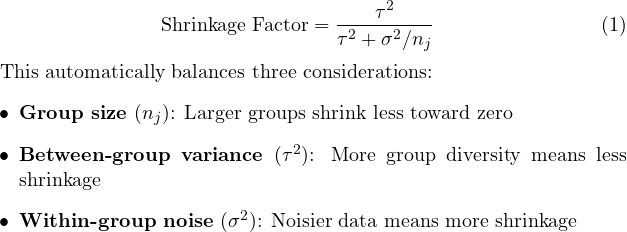
这一公式的重要性在于它实现了数据驱动的最优正则化,无需人工调优超参数。
M步实现:参数更新机制
def _m_step(self, y, X, random_effects):
"""基于当前随机效应估计更新模型参数"""
# 构建随机效应设计矩阵
Z = np.zeros((len(y), self.n_groups))
for i, group in enumerate(self.groups):
group_position = np.where(self.unique_groups == group)[0][0]
Z[i, group_position] = 1
# 更新固定效应(对调整后响应变量的OLS估计)
y_adjusted = y - Z @ random_effects
XtX_inv = np.linalg.inv(X.T @ X + 1e-8 * np.eye(X.shape[1]))
self.beta = XtX_inv @ X.T @ y_adjusted
# 基于矩量法更新方差组件
full_residuals = y - X @ self.beta - Z @ random_effects
self.sigma2 = np.mean(full_residuals**2)
# 从随机效应计算组间方差
self.tau2 = max(0.01, np.mean(random_effects**2))完整EM算法集成
def fit(self, y, X, max_iter=100, tol=1e-6):
"""完整的期望最大化算法实现"""
self._initialize_parameters(y, X)
log_likelihoods = []
for iteration in range(max_iter):
# E步:估计随机效应
random_effects = self._e_step(y, X)
# M步:更新参数
self._m_step(y, X, random_effects)
# 监控收敛过程
loglik = self._compute_log_likelihood(y, X, random_effects)
log_likelihoods.append(loglik)
if len(log_likelihoods) > 1:
if abs(log_likelihoods[-1] - log_likelihoods[-2]) < tol:
print(f"算法在{iteration + 1}次迭代后收敛")
break
self.random_effects = random_effects
self.log_likelihoods = log_likelihoods
return self
def _compute_log_likelihood(self, y, X, random_effects):
"""计算边际对数似然函数"""
Z = np.zeros((len(y), self.n_groups))
for i, group in enumerate(self.groups):
group_position = np.where(self.unique_groups == group)[0][0]
Z[i, group_position] = 1
residuals = y - X @ self.beta - Z @ random_effects
# 简化的对数似然计算(忽略常数项)
ll_data = -0.5 * np.sum(residuals**2) / self.sigma2
ll_random = -0.5 * np.sum(random_effects**2) / self.tau2
return ll_data + ll_random收缩机制的智能适应性
为了直观展示收缩机制的自适应特性,以下代码创建了相应的可视化分析:
def demonstrate_shrinkage_intelligence():
"""展示收缩机制对数据特征的智能适应"""
group_sizes = np.arange(5, 101, 5)
variance_ratios = [0.1, 0.5, 1.0, 2.0, 5.0] # tau2/sigma2
fig, axes = plt.subplots(1, 2, figsize=(15, 6))
# 收缩因子与组大小的关系
for ratio in variance_ratios:
tau2, sigma2 = ratio, 1.0
shrinkage_factors = tau2 / (tau2 + sigma2 / group_sizes)
axes[0].plot(group_sizes, shrinkage_factors,
label=f'τ²/σ² = {ratio}', linewidth=2)
axes[0].set_xlabel('组大小')
axes[0].set_ylabel('收缩因子')
axes[0].set_title('基于组大小的自适应正则化')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
# 实际应用场景示例
small_group_shrinkage = 0.1 / (0.1 + 1.0 / 10) # 小组,低方差比
large_group_shrinkage = 2.0 / (2.0 + 1.0 / 100) # 大组,高方差比
scenarios = ['小组\n低组间差异', '大组\n高组间差异']
shrinkages = [small_group_shrinkage, large_group_shrinkage]
axes[1].bar(scenarios, shrinkages, color=['coral', 'skyblue'])
axes[1].set_ylabel('收缩因子')
axes[1].set_title('数据上下文的自动适应机制')
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 执行可视化
demonstrate_shrinkage_intelligence()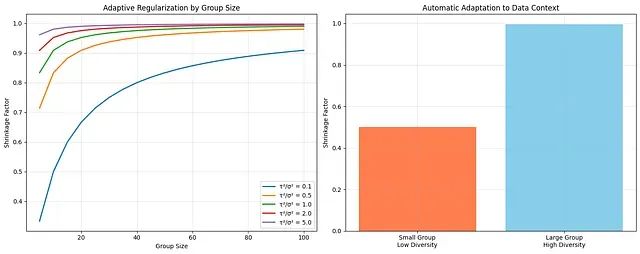
这一可视化揭示了混合效应模型的核心优势:模型能够根据数据的内在特征自动调整正则化策略。对于组间变异较小的小组,模型施加较强的正则化;而对于样本量大且组间差异显著的组,模型则保留更多的个体特征。
现代机器学习应用扩展
理解混合效应模型的内部机制为超越传统统计包处理能力的现代机器学习应用提供了基础。
神经网络架构集成
随机效应概念可以直接启发神经网络层的设计:
class RandomEffectsLayer(torch.nn.Module):
"""融合混合效应思想的神经网络层"""
def __init__(self, n_groups, embedding_dim):
super().__init__()
self.group_embeddings = torch.nn.Embedding(n_groups, embedding_dim)
self.shrinkage = torch.nn.Parameter(torch.tensor(0.5))
def forward(self, x, group_ids):
group_effects = self.group_embeddings(group_ids)
# 应用可学习的收缩机制
shrunk_effects = self.shrinkage * group_effects
return x + shrunk_effects深度学习中的层次化正则化
混合效应的核心思想可以改进任何涉及分组数据的模型:
def hierarchical_regularization_loss(predictions, targets, groups, lambda_within, lambda_between):
"""基于混合效应原理的自定义损失函数"""
base_loss = F.mse_loss(predictions, targets)
# 组内正则化项
within_penalty = 0
for group in torch.unique(groups):
group_mask = groups == group
group_preds = predictions[group_mask]
within_penalty += torch.var(group_preds)
# 组间正则化项(促进收缩效应)
group_means = []
for group in torch.unique(groups):
group_mask = groups == group
group_means.append(torch.mean(predictions[group_mask]))
between_penalty = torch.var(torch.stack(group_means))
return base_loss + lambda_within * within_penalty - lambda_between * between_penalty高级特征工程技术
基于混合效应理论的特征工程能够创建更加精细的预测特征:
def create_shrinkage_features(df, target_col, group_col, features):
"""利用混合效应收缩原理进行特征工程"""
shrinkage_features = {}
for feature in features:
# 计算组特定均值和全局均值
global_mean = df[feature].mean()
group_means = df.groupby(group_col)[feature].mean()
group_sizes = df.groupby(group_col).size()
# 方差组件估计(简化实现)
within_var = df.groupby(group_col)[feature].var().mean()
between_var = group_means.var()
# 应用收缩公式
shrinkage_factors = between_var / (between_var + within_var / group_sizes)
shrunk_means = shrinkage_factors * group_means + (1 - shrinkage_factors) * global_mean
# 生成收缩特征
shrinkage_features[f'{feature}_group_shrunk'] = df[group_col].map(shrunk_means)
return pd.DataFrame(shrinkage_features)REML估计与计算优化
对于生产环境的应用,限制性最大似然(REML)估计通常能提供更好的方差组件估计:
def fit_reml(self, y, X):
"""限制性最大似然估计实现"""
self._initialize_parameters(y, X)
def reml_objective(log_variance_params):
tau2, sigma2 = np.exp(log_variance_params)
total_loglik = 0
for group in self.unique_groups:
group_idx = self.group_indices[group]
y_group = y[group_idx]
X_group = X[group_idx]
n_j = len(group_idx)
# 组协方差矩阵:V = tau2 * J + sigma2 * I
V = tau2 * np.ones((n_j, n_j)) + sigma2 * np.eye(n_j)
try:
V_inv = np.linalg.inv(V)
# REML似然计算(简化版本)
residuals = y_group - X_group @ self.beta
total_loglik += -0.5 * (
residuals.T @ V_inv @ residuals +
np.log(np.linalg.det(V))
)
except np.linalg.LinAlgError:
return 1e10 # 矩阵奇异时返回惩罚值
return -total_loglik
# 方差组件优化
result = minimize(
reml_objective,
x0=[np.log(self.tau2), np.log(self.sigma2)],
method='BFGS'
)
if result.success:
self.tau2, self.sigma2 = np.exp(result.x)
self.random_effects = self._e_step(y, X)
return self实际应用场景
自定义实现通常在以下前沿机器学习应用中发挥关键作用:
领域特定优化:医疗健康数据分析可能需要基于临床意义而非统计阈值的收敛准则,这超出了标准库的预设范围。
混合架构开发:将收缩概念集成到神经网络或集成方法中需要超越传统统计包的算法灵活性。
规模化部署:现代大规模数据集通常需要计算层面的深度优化,包括GPU加速、分布式处理和内存效率优化,这需要对底层算法的深入理解。
实时系统:流式组效应处理或在线学习场景需要标准实现无法支持的算法定制。
总结
从零构建混合效应模型不仅是理论学习,更是技术创新的基础。深入理解数学原理后,可以实现以下技术扩展:通过广义线性混合模型处理非高斯数据;利用稀疏矩阵操作和并行组处理实现大规模数据的高效处理;在集成方法或深度学习框架中融合混合效应概念。
当前数据科学领域正从通用算法向复杂的、领域特定的方法转变。混合效应模型代表了一个成熟的统计框架,为与现代机器学习工作流程的深度集成提供了坚实基础。
当面对分组数据时,深入的理解将使数据科学家跳出传统方法的思维限制。不再局限于"包含组虚拟变量"或"完全忽略组效应"的二元选择,而是能够识别第三种路径:通过学习的、自适应的正则化机制,自动平衡个体组模式与总体趋势。
最重要的认识是,混合效应模型并非神秘的技术,而是普通回归方法在层次化结构建模方面的原理性扩展。这种理解将成为机器学习工具箱中下一个技术突破的重要基础。
https://avoid.overfit.cn/post/ebaa96d3c4f04545b3706bf52da8b6ee



