Winograd算法最早于1980年由Shmuel Winograd在《Arithmetic complexity of computations(1980)》中提出,主要用来减少FIR滤波器的计算量。
该算法类似FFT,将数据映射到另一个空间上,用加减运算代替部分乘法运算,在“加减运算速度远高于乘法运算”的前提下达到明显的加速效果(与FFT不同的是,Winograd将数据映射到一个实数空间而非复数空间)。
比如,
直接实现一个 $m$ 输出、$r$ 参数的FIR滤波器 $F(m,r)$,一共需要 $m \times r$ 次乘法运算;
但使用Winograd算法,忽略变换过程的话,仅仅需要 $m + r - 1$ 次乘法运算。
$F(2,3)$
如果直接计算 $F(2,3)$:
$$ F(2,3)=\left[\begin{array}{lll}{d_{0}} & {d_{1}} & {d_{2}} \\ {d_{1}} & {d_{2}} & {d_{3}}\end{array}\right]\left[\begin{array}{l}{g_{0}} \\ {g_{1}} \\ {g_{2}}\end{array}\right]=\left[\begin{array}{l}{d_0g_0+d_1g_1+d_2g_2} \\ {d_1g_0+d_2g_1+d_3g_2}\end{array}\right] $$
其中,
$d_0, d_1, d_2$和$d_1, d_2, d_3$为连续的两个输入序列;
$g_0, g_1, g_2$为FIR的三个参数;
这个过程一共需要6次乘法,和4次加法
而Winograd算法指出,$F(2,3)$ 可以这样计算:
$$ F(2,3)=\left[\begin{array}{lll}{d_{0}} & {d_{1}} & {d_{2}} \\ {d_{1}} & {d_{2}} & {d_{3}}\end{array}\right]\left[\begin{array}{l}{g_{0}} \\ {g_{1}} \\ {g_{2}}\end{array}\right]=\left[\begin{array}{l}{m_{1}+m_{2}+m_{3}} \\ {m_{2}-m_{3}-m_{4}}\end{array}\right] $$
其中,
$$ \begin{array}{ll}{m_{1}=\left(d_{0}-d_{2}\right) g_{0}} & {m_{2}=\left(d_{1}+d_{2}\right) \frac{g_{0}+g_{1}+g_{2}}{2}} \\ {m_{4}=\left(d_{1}-d_{3}\right) g_{2}} & {m_{3}=\left(d_{2}-d_{1}\right) \frac{g_{0}-g_{1}+g_{2}}{2}}\end{array} $$
该用矩阵运算可以表示成:
$$ Y=A^{T}\left[(G g) \odot\left(B^{T} d\right)\right] $$
其中,$\odot$表示点乘,而
$$ B^{T}=\left[\begin{array}{rrrr}{1} & {0} & {-1} & {0} \\ {0} & {1} & {1} & {0} \\ {0} & {-1} & {1} & {0} \\ {0} & {1} & {0} & {-1}\end{array}\right], G=\left[\begin{array}{rrr}{1} & {0} & {0} \\ {\frac{1}{2}} & {\frac{1}{2}} & {\frac{1}{2}} \\ {\frac{1}{2}} & {-\frac{1}{2}} & {\frac{1}{2}} \\ {0} & {0} & {1}\end{array}\right], A^{T}=\left[\begin{array}{rrrr}{1} & {1} & {1} & {0} \\ {0} & {1} & {-1} & {-1}\end{array}\right] $$
$$ g=\left[\begin{array}{lll}{g_{0}} & {g_{1}} & {g_{2}}\end{array}\right]^{T}, d=\left[\begin{array}{llll}{d_{0}} & {d_{1}} & {d_{2}} & {d_{3}}\end{array}\right]^{T} $$
这……似乎反而把问题变得十分复杂,但实际上它的计算量却真真切切地减少了——
- 由于$g$是固定的FIR滤波器参数,那么$Gg$可以提前计算并得到一个 $4\times1$ 的列向量
- 由于$d$是变化的输入序列,所以每次计算FIR的时候都需要对输入$d$做一个变换$B^Td$,得到一个 $4 \times 1$ 的列向量,这个过程需要4次加法(注意$B^T$矩阵的元素值)
- 然后$Gg$和$B^Td$进行点乘,共计4次乘法
- 最后$A^T$与$[(Gg)\odot(B^Td)]$做乘法,共计4次加法
过程1可以提前完成,变换过程2和计算过程3、4共计4次乘法和8次加法,相比于直接FIR的6次乘法、4次加法,乘法次数下降为原来的$\frac{2}{3}$(推广到一般情况,直接FIR跟Winograd的乘法次数分别是$m \times r$和$m+r-1$)。
但天下没有免费的午餐,既然速度得到提升,那么肯定需要付出代价——算法的加速往往是需要以额外的空间为代价的:原先FIR只需要存储3个参数$g$,但现在需要存储4个参数$Gg$(推广到一般情况,分别是$r$和$m+r-1$);
$F(2\times2, 3\times3)$
参考arm的一份幻灯片:Even Faster CNNs: Exploring the New Class of Winograd Algorithms
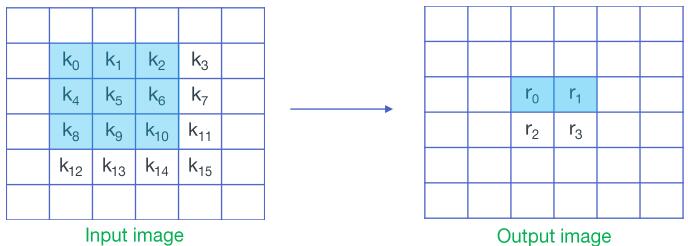
接下来我们将一维的$F(2,3)$扩展到二维的$F(2\times2, 3\times3)$,有两种扩展方式,一是通过堆叠$F(2,3)$来实现$F(2\times2, 3\times3)$,二是通过嵌套$F(2,3)$来实现$F(2\times2, 3\times3)$。后者计算量减小幅度更大,但前者占用内存更少。以k3s1的卷积为例——
为了跟幻灯片的符号统一,在这一部分中用$k$来表示输入,$w$表示权重,$r$表示输出
$$ W = \left[\begin{array}{lll}{w_{0}} & {w_{1}} & {w_{2}} \\ {w_{3}} & {w_{4}} & {w_{5}} \\ {w_{6}} & {w_{7}} & {w_{8}}\end{array}\right] $$
对直接卷积来说,该过程一共需要36次乘法和32次加法。
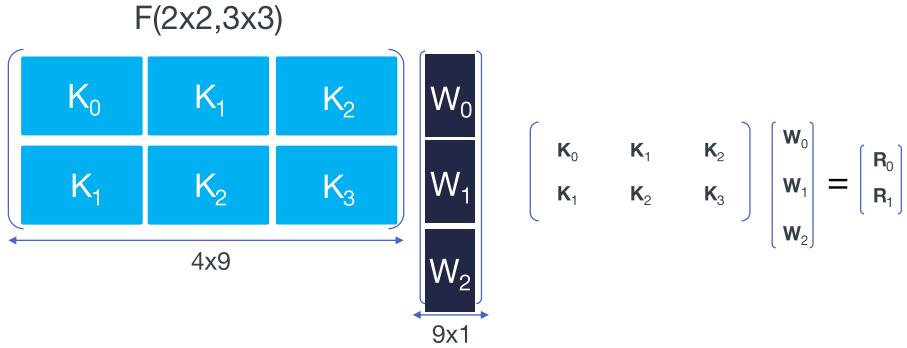
参考Even Faster CNNs: Exploring the New Class of Winograd Algorithms,将输入按滑窗分块后展开成向量并堆叠成矩阵,将权重展开成向量—— 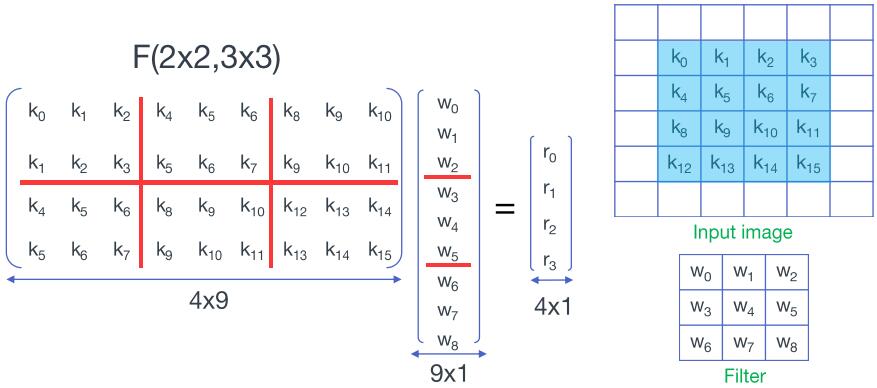
对矩阵和向量进行分块——
堆叠实现
$$ \begin{aligned} \left[\begin{array}{lll}{K_0} & {K_1} & {K_2} \\ {K_1} & {K_2} & {K_3} \end{array}\right] \left[\begin{array}{l}{W_0} \\ {W_1} \\ {W_2} \end{array}\right] &= \left[\begin{array}{l}{R_0} \\ {R_1} \end{array}\right] = \left[\begin{array}{l}{K_0W_0+K_1W_1+K_2W_2} \\ {K_1W_0+K_2W_1+K_3W_2} \end{array}\right] \\ \\ &= \left[\begin{array}{l}{F_{(2,3)}(D_0,W_0)+F_{(2,3)}(D_1,W_1)+F_{(2,3)}(D_2,W_2)} \\ {F_{(2,3)}(D_1,W_0)+F_{(2,3)}(D_2,W_1)+F_{(2,3)}(D_3,W_2)} \end{array}\right] \end{aligned} $$
其中,$D_i$是$K_i$对应的输入序列,也即卷积输入的第$i$行
$$ D = \left[\begin{array}{llll} {k_0} & {k_4} & {k_8} & {k_{12}} \\ {k_1} & {k_5} & {k_9} & {k_{13}} \\ {k_2} & {k_6} & {k_{10}} & {k_{14}} \\ {k_3} & {k_7} & {k_{11}} & {k_{15}} \end{array}\right] = \left[\begin{array}{l} D_0 & D_1 & D_2 & D_3 \end{array}\right] $$
也就是说,$F(2\times2, 3\times3)$在这里分成了6次$F(2,3)$以及4次额外的加法,总计24次乘法和44次加法(注意:虽然这里做了6次$F(2,3)$但是输入序列的变换只需要做4次,所以加法次数是44次而非52次),相比于直接卷积的36次乘法和32次加法,乘法次数跟一维的$F(2,3)$一样,也下降为原来的$\frac{2}{3}$,同理也需要付出3倍于$F(2,3)$额外的空间代价(三个$W$):
嵌套实现
参考《卷积神经网络中的Winograd快速卷积算法 | shinelee, 博客园》
$$ \begin{aligned} \left[\begin{array}{lll}{K_0} & {K_1} & {K_2} \\ {K_1} & {K_2} & {K_3} \end{array}\right] &= \left[ \begin{array}{c}{R_0} \\ {R_1}\end{array}\right] = \left[ \begin{array}{c}{K_0 W_0 + K_1 W_1 + K_2 W_2} \\ {K_1 W_0 + K_2 W_1 + K_3 W_2} \end{array} \right] \\ \\ &= \left[\begin{array}{l}{F_{(2,3)}(D_0,W_0)+F_{(2,3)}(D_1,W_1)+F_{(2,3)}(D_2,W_2)} \\ {F_{(2,3)}(D_1,W_0)+F_{(2,3)}(D_2,W_1)+F_{(2,3)}(D_3,W_2)} \end{array}\right] \\ &= \left[ \begin{array}{c} {A^{T}\left[(G W_0) \odot\left(B^{T} D_0 \right)\right] + A^{T}\left[(G W_1) \odot\left(B^{T} D_1 \right)\right] + A^{T}\left[(G W_2) \odot\left(B^{T} D_2 \right)\right]} \\ {A^{T}\left[(G W_0) \odot\left(B^{T} D_1 \right)\right] + A^{T}\left[(G W_1) \odot\left(B^{T} D_2 \right)\right] + A^{T}\left[(G W_2) \odot\left(B^{T} D_3 \right)\right]} \end{array} \right] \\ \\ &=A^{T}\left[\left[G [W_0 \ W_1 \ W_2 ] G^{T}\right] \odot\left[B^{T} [D_0 \ D_1 \ D_2 \ D_3] B\right]\right]A \\ \\ &=A^{T}\left[\left[G w G^{T}\right] \odot\left[B^{T} d B\right]\right] A \\ \\ &\textit{(...w => g...)} \\ \\ &=A^{T}\left[\left[G g G^{T}\right] \odot\left[B^{T} d B\right]\right] A \end{aligned} $$
也即,
$$F(2\times2, 3\times3) = A^{T} \left[ U \odot V \right] A$$
其中,
$$U = G g G^{T}$$
$$V = B^{T} d B$$
与$F(2,3)$同理,可以推导出,$F(2\times2, 3\times3)$需要16次乘法和56次加法($V=B^{T} d B$过程32次加法、$M=U \odot V$过程16次乘法、$Y=A^TMA$过程24次加法),相比于直接卷积的36次乘法和32次加法,乘法次数下降为原来的$\frac{16}{36}$。计算量的减少比堆叠实现要明显,但也需要更多的额外空间代价:直接计算只需要存储9个参数的$g$,$F(2\times2,3\times3)$则需要存储16个参数的$GgG^T$(推广到一般情况,分别为$r^2$和$(r+m-1)^2$)
$G$、$B^T$、$A^T$
Winograd算法需要推导出相应的变换矩阵$G$、$B^T$和$A^T$,但具体的推导过程似乎有些复杂,我现在还没弄懂。所幸 wincnn | github提供了一个解算$G$、$B^T$、$A^T$的工具,除了前述的$F(2,3)$,常用的还有$F(4,3)$和$F(6,3)$,它们对应的变换矩阵如下:
$F(4,3)$
$$ B^{T}=\left[\begin{array}{rrrrrr} {4} & {0} & {-5} & {0} & {1} & {0} \\ {0} & {-4} & {-4} & {1} & {1} & {0} \\ {0} & {4} & {-4} & {-1} & {1} & {0} \\ {0} & {-2} & {-1} & {2} & {1} & {0} \\ {0} & {2} & {-1} & {-2} & {1} & {0} \\ {0} & {4} & {0} & {-5} & {0} & {1} \end{array}\right], G=\left[\begin{array}{rrr} {1/4} & {0} & {0} \\ {-1/6} & {-1/6} & {-1/6} \\ {-1/6} & {1/6} & {-1/6} \\ {1/24} & {1/12} & {1/6} \\ {1/24} & {-1/12} & {1/6} \\ {0} & {0} & {1} \end{array}\right], \\ A^{T}=\left[\begin{array}{rrrrrr} {1} & {1} & {1} & {1} & {1} & {0} \\ {0} & {1} & {-1} & {2} & {-2} & {0} \\ {0} & {1} & {1} & {4} & {4} & {0} \\ {0} & {1} & {-1} & {8} & {-8} & {1} \end{array}\right] $$
$$ g=\left[\begin{array}{lll}{g_{0}} & {g_{1}} & {g_{2}}\end{array}\right]^{T}, d=\left[\begin{array}{llllll}{d_{0}} & {d_{1}} & {d_{2}} & {d_{3}} & {d_4} & {d_5}\end{array}\right]^{T} $$
$F(6,3)$
$$ B^{T}=\left[\begin{array}{rrrrrrrr} {1} & {0} & {-21/4} & {0} & {21/4} & {0} & {-1} & {0} \\ {0} & {1} & {1} & {-17/4} & {-17/4} & {1} & {1} & {0} \\ {0} & {-1} & {1} & {17/4} & {-17/4} & {-1} & {1} & {0} \\ {0} & {1/2} & {1/4} & {-5/2} & {-5/4} & {2} & {1} & {0} \\ {0} & {-1/2} & {1/4} & {5/2} & {-5/4} & {-2} & {1} & {0} \\ {0} & {2} & {4} & {-5/2} & {-5} & {1/2} & {1} & {0} \\ {0} & {-2} & {4} & {5/2} & {-5} & {-1/2} & {1} & {0} \\ {0} & {-1} & {0} & {21/4} & {0} & {-21/4} & {0} & {1} \end{array}\right], \\ G=\left[\begin{array}{rrr} {1} & {0} & {0} \\ {-2/9} & {-2/9} & {-2/9} \\ {-2/9} & {2/9} & {-2/9} \\ {1/90} & {1/45} & {2/45} \\ {1/90} & {-1/45} & {2/45} \\ {32/45} & {16/45} & {8/45} \\ {32/45} & {-16/45} & {8/45} \\ {0} & {0} & {1} \end{array}\right], \\ A^{T}=\left[\begin{array}{rrrrrrrr} {1} & {1} & {1} & {1} & {1} & {1} & {1} & {0} \\ {0} & {1} & {-1} & {2} & {-2} & {1/2} & {-1/2} & {0} \\ {0} & {1} & {1} & {4} & {4} & {1/4} & {1/4} & {0} \\ {0} & {1} & {-1} & {8} & {-8} & {1/8} & {-1/8} & {0} \\ {0} & {1} & {1} & {16} & {16} & {1/16} & {1/16} & {0} \\ {0} & {1} & {-1} & {32} & {-32} & {1/32} & {-1/32} & {1} \\ \end{array}\right] $$
$$ g=\left[\begin{array}{lll}{g_{0}} & {g_{1}} & {g_{2}}\end{array}\right]^{T}, d=\left[\begin{array}{llllll}{d_{0}} & {d_{1}} & {d_{2}} & {d_{3}} & {d_4} & {d_5} & {d_6} & {d_7}\end{array}\right]^{T} $$
注意:与$F(2,3)$不同,由于$F(4,3)$和$F(6,3)$的$A^T$、$B^T$出现了非$[0,1,-1]$的元素,所以除了点乘过程,还会引入额外的乘法运算。
比较
接下来我们对$F(2,3)$、$F(4,3)$、$F(6,3)$、$F(2\times2,3\times3)$、$F(4\times4,3\times3)$、$F(6\times6,3\times3)$的效果做一简单比较。
| Winograd | 原始乘法次数 | Win乘法次数 | 理论加速比 | 乘法加速比(含变换) | 原始内存 | Win内存 | 内存增长 |
|---|---|---|---|---|---|---|---|
| $F(2,3)$ | 6 | 4(4) | 1.50 | 1.50 | 3 | 4 | 1.33 |
| $F(4,3)$ | 12 | 12(6) | 2.00 | 1.00 | 3 | 6 | 2.00 |
| $F(6,3)$ | 18 | 28(8) | 2.25 | 0.64 | 3 | 8 | 2.67 |
| 堆$F(2\times2,3\times3)$ | 36 | 24(24) | 1.50 | 1.50 | 9 | 12 | 1.33 |
| 堆$F(4\times4,3\times3)$ | 144 | 126(72) | 2.00 | 1.14 | 9 | 18 | 2.00 |
| 堆$F(6\times6,3\times3)$ | 324 | 396(144) | 2.25 | 0.82 | 9 | 24 | 2.67 |
| 嵌$F(2\times2,3\times3)$ | 36 | 16(16) | 2.25 | 2.25 | 9 | 16 | 1.78 |
| 嵌$F(4\times4,3\times3)$ | 144 | 48(36) | 4.00 | 3.00 | 9 | 36 | 4.00 |
| 嵌$F(6\times6,3\times3)$ | 324 | 102(64) | 5.06 | 3.18 | 9 | 64 | 7.11 |
以上数据是我自己手推的,可能有不正确的地方,欢迎指正~
Win乘法次数列括号内表示不考虑变换产生的乘法运算(即仅考虑点乘的乘法)- 注意,在$V = B^{T} d B$和$Y = A^T M A$的计算过程中,$A^T$或$B^T$矩阵内元素绝对值相同的乘法运算其实是可以合并的
- 从理论的乘法加速比来看(只考虑点乘的乘法),Winograd都有相当理想的加速效果,嵌套实现的$F(6\times6,3\times3)$甚至有5.06倍的加速
- 但考虑到$V = B^{T} d B$和$Y = A^T M A$的计算过程中也有大量的乘法,实际乘法加速效果并没有那么高,嵌套实现的$F(6\times6,3\times3)$其实也只有3.12倍的加速效果;$F(6,3)$和堆叠实现的$F(6\times6,3\times3)$反而出现明显的减速;
- $F(2,3)$和$F(2\times2, 3\times3)$非常有意思,其$A^T$矩阵和$B^T$矩阵的元素均为$[0,1,-1]$——也就是说在变换过程中不会产生额外的乘法开销
- 从额外的内存开销上来看(仅考虑参数占用的内存),二维大于一维、嵌套实现大于堆叠实现
- 尽管$V = B^{T} d B$和$Y = A^T M A$的计算过程中也有大量的乘法,但观察可以发现$F(4,3)$和$F(6,3)$的$A^T$矩阵和$B^T$中有相当多的元素恰好是$2^n$,也就是说,用Winograd计算量化的卷积应该会有神奇的加成(对浮点运算来说,能否直接通过对指数部分做加法实现??)
Winograd卷积
以上介绍了一维和二维的Winograd算法,但实际在神经网络的特征图却通常都是三维的,没法直接往上套。不过前文在介绍二维Winograd的时候,我们除了嵌套之外还用了堆叠一维Winograd来达到二维Winograd的结果,同样的也可以用堆叠的二维Winograd来将其应用到三维的卷积当中。
前述只讨论了一些比较简单的情况,事实上在CNN中,由于输入的特征图只需要变换一次,而却会被多个滤波器复用,所以输入变换过程的额外开销会被平摊——卷积的滤波器(也即输出通道)越多,那么输入变换产生的额外开销的影响就越小。
至于特征图的额外空间代价,嵌套实现的$F(m \times m,r \times r)$会产生$(\frac{m+r-1}{m})^2$倍的内存占用(相比之下im2col则为$r^2$倍)。