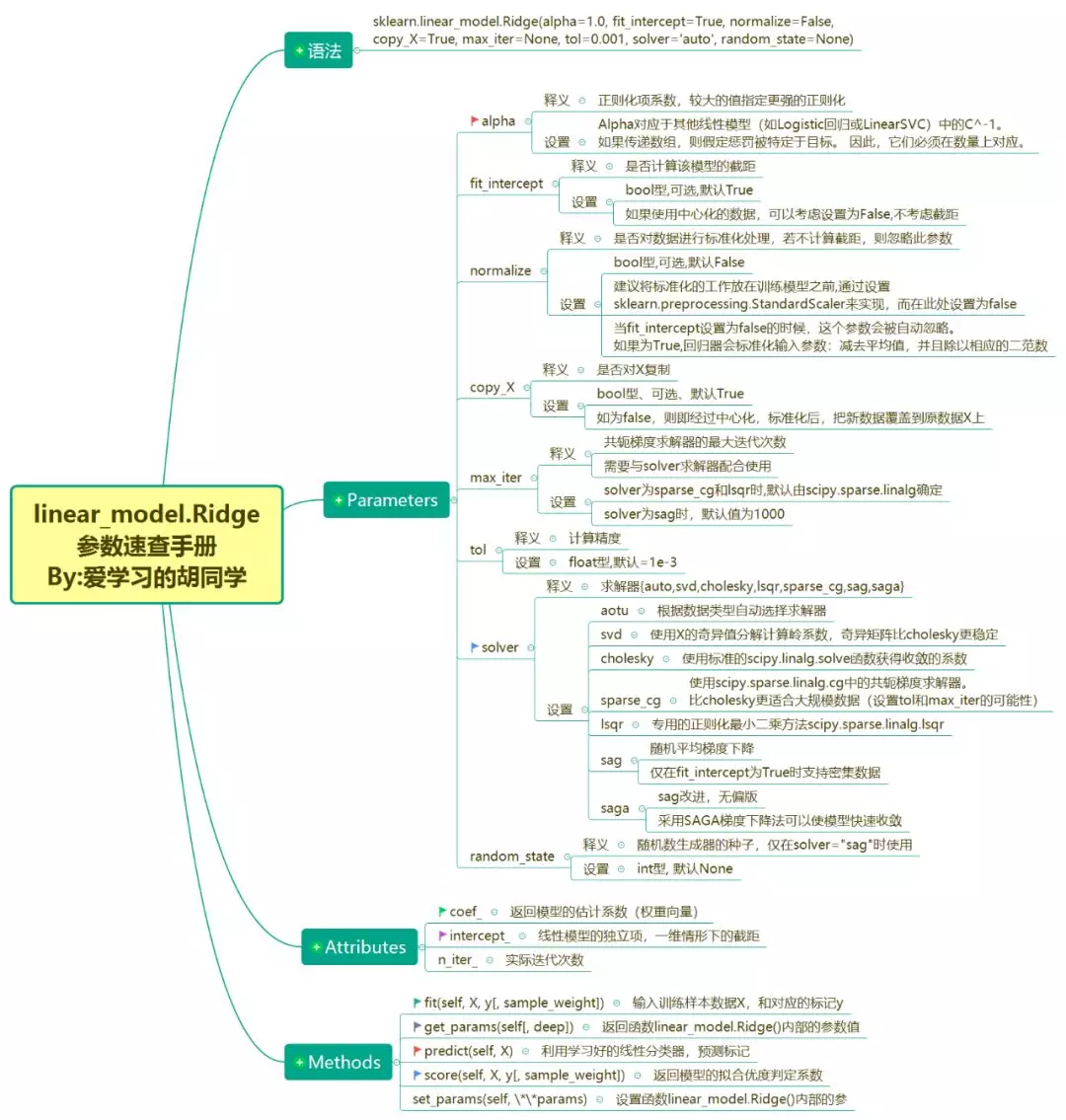
Ridge回归 sklearn API参数速查手册
语法
sklearn.linear_model.Ridge(alpha=1.0,
fit_intercept=True, normalize=False,
copy_X=True, max_iter=None, tol=0.001,
solver='auto', random_state=None)
Parameters
alpha
释义: 正则化项系数,较大的值指定更强的正则化
设置:Alpha对应于其他线性模型(如Logistic回归或LinearSVC)中的C^-1。如果传递数组,则假定惩罚被特定于目标。因此,它们必须在数量上对应。
fit_intercept
释义:是否计算该模型的截距
设置:bool型,可选,默认True;如果使用中心化的数据,可以考虑设置为False,不考虑截距
normalize
释义:是否对数据进行标准化处理,若不计算截距,则忽略此参数
设置:bool型,可选,默认False,建议将标准化的工作放在训练模型之前,通过设置sklearn.preprocessing.StandardScaler来实现,而在此处设置为false;当fit_intercept设置为false的时候,这个参数会被自动忽略。如果为True,回归器会标准化输入参数:减去平均值,并且除以相应的二范数
copy_X
释义:是否对X复制
设置:bool型、可选、默认True;如为false,则即经过中心化,标准化后,把新数据覆盖到原数据X上
max_iter
释义:共轭梯度求解器的最大迭代次数,需要与solver求解器配合使用
设置:solver为sparse_cg和lsqr时,默认由scipy.sparse.linalg确定,solver为sag时,默认值为1000
tol
释义:计算精度
设置:float型,默认=1e-3
solver
释义:求解器{auto,svd,cholesky,lsqr,sparse_cg,sag,saga}
设置:
aotu:根据数据类型自动选择求解器
svd:使用X的奇异值分解计算岭系数,奇异矩阵比cholesky更稳定
cholesky:使用标准的scipy.linalg.solve函数获得收敛的系数
sparse_cg:使用scipy.sparse.linalg.cg中的共轭梯度求解器。比cholesky更适合大规模数据(设置tol和max_iter的可能性)
lsqr:专用的正则化最小二乘方法scipy.sparse.linalg.lsqr
sag:随机平均梯度下降;仅在fit_intercept为True时支持密集数据
saga:sag改进,无偏版.采用SAGA梯度下降法可以使模型快速收敛
random_state
释义:随机数生成器的种子,仅在solver="sag"时使用
设置:int型, 默认None
Attributes
coef_
返回模型的估计系数(权重向量)
intercept_
线性模型的独立项,一维情形下的截距
n_iter_
实际迭代次数
Methods
fit(self, X, y[, sample_weight])
输入训练样本数据X,和对应的标记y
get_params(self[, deep])
返回函数linear_model.Ridge()内部的参数值
predict(self, X)
利用学习好的线性分类器,预测标记
score(self, X, y[, sample_weight])
返回模型的拟合优度判定系数
set_params(self, **params)
设置函数linear_model.Ridge()内部的参数
本文由博客一文多发平台 OpenWrite 发布!