首发:https://zhuanlan.zhihu.com/p/86004782
作者:张新栋
上一篇文章跟大家介绍了卷积Op的求导过程,熟悉卷积的同学不难发现,conv2d实际上是对input feature进行spatial空间的采样(sliding-window的采样方式)。本文打算跟大家介绍另外一种形式的卷积,dw卷积,其在sliding-windows的采样基础上(spatial sparse),增加了对channels的采样策略(channel sparse)。我们看如下一个简单的例子(左为dw卷积核,右边为input feature):
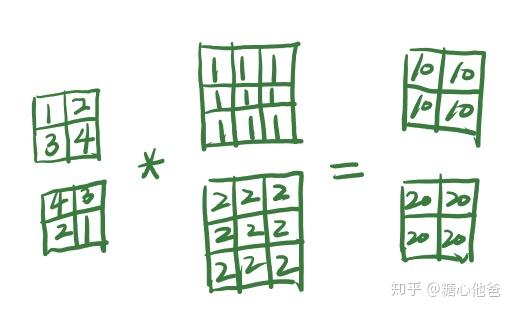
看过之前文章的同学可能知道,如果想对特定Op进行求导,我们之前介绍的方式是,先将该Op转化成线性表达式,所以下面我们将上述dw卷积过程转化成线性表达式,首先我们先看一下输出y关于输入x的求导
- 关于x的求导
针对上面的算例,我们先将其转化成线性表达式,我们希望其能转化成如下形式,偏导数很容易求得:
下面可以看一下转化后的结果:
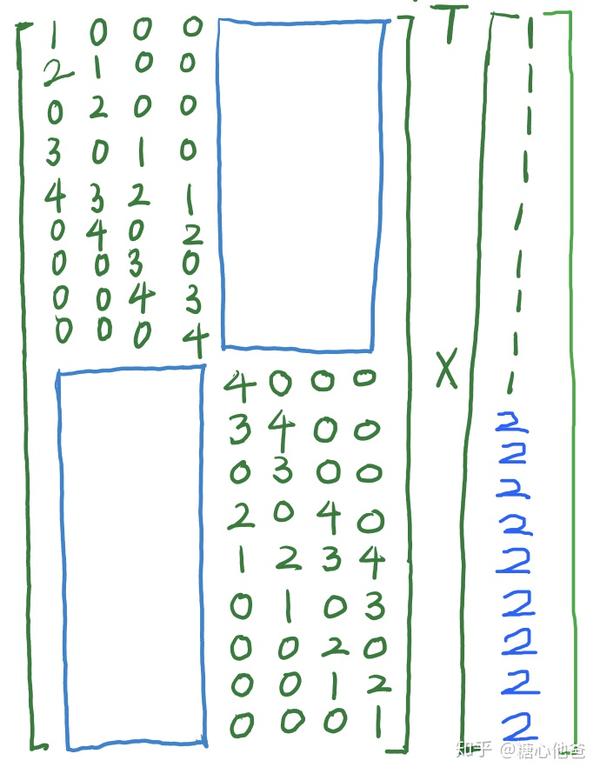
线性表达式-1
上图中的蓝色 矩形内部的元素均为0,也对应了我们之前提到过的dw卷积实际上对应channel sparse的采样策略。
- 关于k的求导
关于k的求导,我们也要将其转化成对应的线性表达式,如:

下面我们看看转化后的线性表达式:
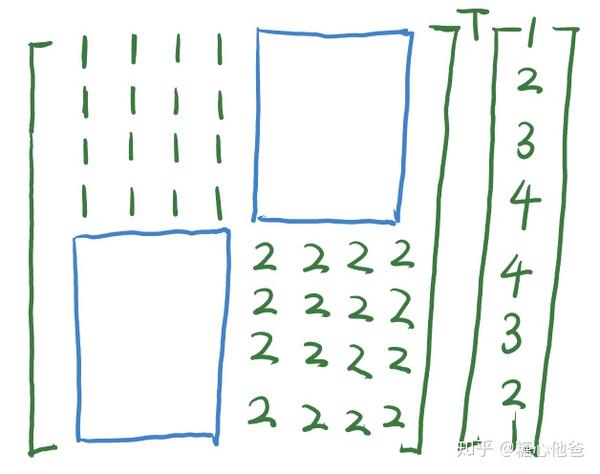
线性表达式-2
- 最后
DW卷积在spatial sparse的基础上增加了channel sparse的采样策略,本文中我们同样将y关于x和dw卷积核k的偏导计算,转化成了对应的线性表达式。我们可以很容易的在转化后的线性表达式上进行对应元素的偏导计算。最后,欢迎大家留言讨论、关注专栏,谢谢大家!
推荐阅读
专注嵌入式端的AI算法实现,欢迎关注作者微信公众号和知乎嵌入式AI算法实现专栏。
更多嵌入式AI相关的技术文章请关注极术嵌入式AI专栏




