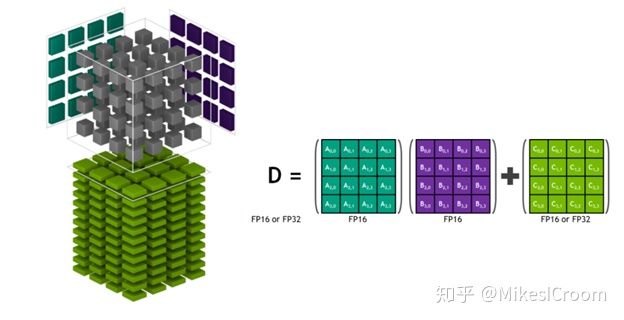
卷积和矩阵乘累加运算是深度学习算法的核心，占据了90%以上的运算。这也是绝大多数硬件加速器的着眼点所在。本文通过对卷积和矩阵乘累加的通用算法的介绍，结合具体的应用场景，分析其在硬件实现和调度上的优劣，希望能对今后的设计有所启发。
作者：MikesICroom
原文：https://zhuanlan.zhihu.com/p/83067033
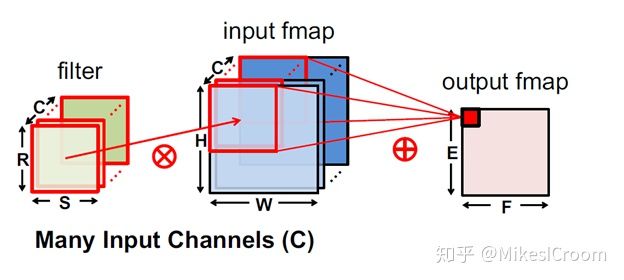
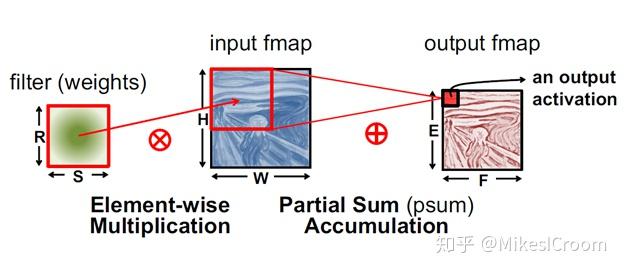
最直接的方式就是直接进行滑动运算，通常采用systolic的计算方法。由于卷积运算的规律性，以及kernel size不变的特征，将kernel数据固定在执行单元中，feature map的数据在执行单元中滑动，每次对覆盖部分做相应的点乘运算。虽然没有减少乘累加的运算量，但很好的进行了kernel的复用，只需pipelined将fmap数据输入执行单元。同时利用output channel方向上的独立性和复用性，流动的fmap数据依次经过多个output channel，在数据流的垂直方向计算生成独立的结果。这就是著名的TPU计算卷积的基本方式了。具体细节网上有很多介绍，这里不再赘述。总结下systolic滑动卷积计算的特点：
1） 很好的利用了kernel的复用性和output channel的独立性，减少了数据带宽的需求
2） 数据流方向和计算流方向正交，两者完全独立，有利于统一的数据流控制和避免读写冲突
3） 结构规则可扩展，利于后端布局和时序调整，可以支持很大规模的硬件实现
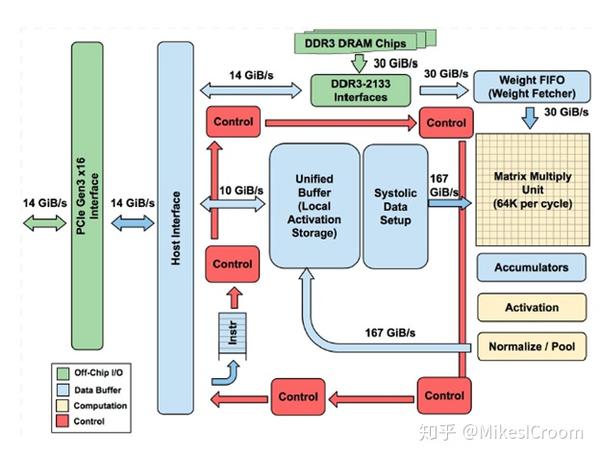因此该方法一直是很多加速器的首选。当然它也有自身的局限性。首先是systolic运算准备时间较长，因此需要较大的执行矩阵和较多的数据量才能隐藏掉准备时间的损失，可以看到TPU的矩阵都是128^2起步的，这样对于较小的算力场景就不是很适合。第二，数据流需要根据卷积滑动方向提前进行调整，这会占用计算时间。TPU采用了独立的systolic data setup模块进行实时调整，这是不小的硬件代价。第三，滑动计算的专用性很强，对于其他类型的运算基本上很难进行数据流的映射，因此需要单独的模块来支持。这样的结构通用性较差。第四，滑动运算需要直接从片上RAM读取数据进行执行才能满足其数据带宽的需求，结果也是直接写回到RAM中，这样就不是通常寄存器结构的编程模型了，需要专门的软件进行优化调度。失去了通用编程框架的硬件也缺乏灵活性。
换一种思路，由于卷积是kernel覆盖内的乘累加运算，这种运算形式在通用处理器上加速效果较差，主要问题是无法很好的利用数据的复用性和局部性。而对于矩阵乘运算，使用GEMM通常可以获得不错的加速效果。因此将卷积转化为矩阵乘运算，不但是CPU、GPU等通用处理器常采用的加速方法，也是很多硬件加速器的选择，可以同时高效的支持卷积和全连接（矩阵乘累加）运算，比如华为的达芬奇，以及NVIDIA的tensor core就是这种方法。具体来讲，就是将三维的kernel在input channel方向展开成2维结构，同时feature map也根据kernel的展开形式打平成对应的2维矩阵，两者进行标准的矩阵乘累加运算就可以实现卷积操作。
GEMM实现有很多好处。首先算法上很成熟，对于硬件和数据的局部性和复用性都处理的很好，在CPU和GPU上的加速效果十分明显，是一个跨平台的通用加速方法。其次，矩阵乘累加本身也具有很好的数据复用性，可以使用包括systolic结构在内的硬件结构进行加速，同样具有滑动方式的优点。第三，通过将大矩阵拆分成小单位矩阵进行运算，可以以很小的数据带宽一次性计算出若干个单位矩阵的乘累加结果，派生出类似tensor core的Cube运算结构，具有很好的扩展性。第四，cube结构下，运算单元较滑动法要紧凑的多，可以以更小的面积换取更大的算力，而且较小的cube不受启动时间的影响，对于各个算力级别的应用场景都有较好的支持。这也是华为的达芬奇采用cube结构的主要原因。
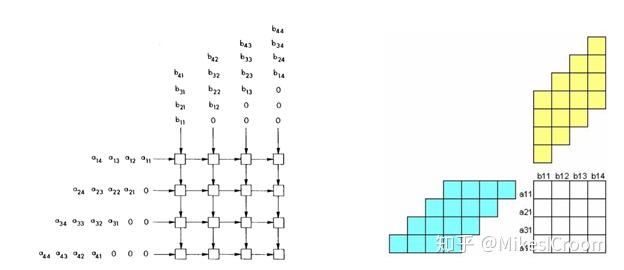
当然GEMM也有缺点。最大的问题是feature map依kernel方向展开后，会出现大量的重复数据，相比滑动法的数据复用性要差不少，相当于用较大的算力弥补了数据冗余的缺陷。因此同等规模下，GEMM硬件加速器的功耗要较滑动法大。第二，平面结构的矩阵运算，不论是systolic，还是cannon's algorithm，结果都累加在执行矩阵中，这样每次运算完成，需要将数据从执行矩阵中读出来，然后才能进行下一次的运算。当然采用ping-pong buffer可以隐藏掉这部分延迟，但控制上要较滑动法复杂不少。第三，kernel和feature map都需要进行二维展开，尤其是feature map需要进行数据的复制调整，这部分是不小的存储代价，需要小心调度，使数据调整和运算能够并行执行。
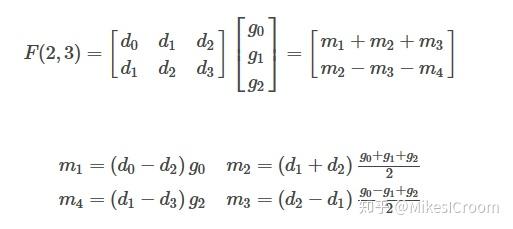除此之外，winograd快速卷积法也在很多框架中广泛应用，具体步骤可以在网上自行搜索。这是一种很特别的思路，简单来讲是通过增加加法运算来减少乘法运算，而在kernel部分的加法可以提前计算（推理过程），这样在整体的运算数量就会下降。注意到winograd算法主要在CPU和GPU平台的深度学习框架中使用，在硬件加速器设计中鲜有所闻。这是由于经过winograd变换后的feature map结构不具有利于大规模硬件计算的规律性，仅可以在一维运算结构的GPU或者CPU上获得运算减少的优势，这样很难使用2维计算矩阵来提高计算密度。其次，winograd同样需要额外的转换和存储，对于较大的feature map还需要切分成很小的tile进行计算，同样限制了加速器的规模。因此winograd方法更适合于面向小算力的一维运算结构，比如带有SIMD或者vector的通用处理器。
总结一下，三种加速方式都有各自适合的应用领域。现在的硬件加速器设计一直在“大力出奇迹”，以堆叠算力为核心竞争力，而这样的规模往往面临着软件调度上的问题。由于大多缺少实际应用的检验和迭代，这样的加速器通常只能在benchmark上表现出最佳状态。这也是在层出不穷的数百T规模加速器的挑战下，NVIDIA的GPU能一直保持绝对优势的原因。十余年在CUDA上的持续优化，是GPU能在任何模型上都有很好的性能的保证。在云服务领域，能够提供通用的高性能至关重要，目前的加速器似乎都缺少了这一点。而在端侧，由于可以只面向专用领域，偏科的硬件加速器更容易获得发挥空间。比如自动驾驶，只需高效完成图像识别和判断就能胜任，这样在算法模型相对固定的情况下，硬件加速器的优势就会凸显。因此，在端侧领域，通用和专用芯片之争，还会继续持续下去。
[1] 文中图片来源于斯坦福大学CS217课程
推荐阅读
更多AI处理器架构设计的技术干货，欢迎关注公众号MikesICroom，
同时欢迎关注AI处理器架构设计专栏。
