HDLBits：在线学习 Verilog （十四 · Problem 65-69） - 极术社区

本系列文章将和读者一起巡礼数字逻辑在线学习网站 HDLBits 的教程与习题，并附上解答和一些作者个人的理解，相信无论是想 7 分钟精通 Verilog，还是对 Verilog 和数电知识查漏补缺的同学，都能从中有所收获。
转载自：知乎

首先附上传送门：

Problem 65 : Half adder (Hadd)

牛刀小试

本题中需要实现一个 2 进制 1bit 加法器，加法器将输入的两个 1bit 数相加，产生两数相加之和以及进位。

解答与分析

module top_module( 
    input a, b,
    output cout, sum );
    assign {cout,sum} = a + b;
endmodule

本题可以先声明一个 2bit 宽度的变量用于接收相加的结果以及可能的进位，2 个 1bit 数相加可能产生一个 2bit 宽度的结果。将高位赋予 cout，低位赋予 sum。

也可以像上方的解答一样，使用位连接符语法，省去显示的变量信号声明。

Problem 66 : Full adder (Fadd)

牛刀小试

本题中需要实现一个 2 进制 1bit 全加器，全加器与上一题中的加法器的区别在于，除了将输入的两个 1bit 数相加之外，还累加来自前级的进位，产生相加之和以及进位。

解答与分析

module top_module( 
    input a, b, cin,
    output cout, sum );
    assign{cout,sum} = a + b + cin;
endmodule

与上一题的半全加器相比，一般全加器才是数字系统中广泛使用的加法器。这里的 1bit 全加器往往会并行构成更宽的全加器。

Problem 67 : 3-bit binary adder(Adder3 )

牛刀小试

在上一题中，我们实现了一个全加器，本题中需要通过实例化 3 个全加器，并将它们级联起来实现一个位宽为 3 bit 的二进制加法器，加法器将输入的两个 3bit 数相加，产生相加之和以及进位。

这里分析一下：一个 3bit 全加器由 3 个 1bit 全加器组成，每一比特位对应一个全加器。涉及到进位时，假设最低位产生进位，那个一个 1'b1 就会加到更高 1bit 的全加器中。信号连接时，最低位的 cout 就是次低位的 cin 信号，以此类推。

可以注意到题目给出的模块端口中，cout 的宽度为 3bit ，实际的 3-bit 全加器的进位应该为最高位的 1 bit 进位。这里的 cout 其实包括了每一位上的进位，作者的意思是为了鼓励大家真的例化 3 个全加器模块。并将每个全加器的 cout 连接到输出 cout 中。不然的话 assign {cout,sum} = a + b + cin; 就能 pass 这道题。

解答与分析

module top_module( 
    input [2:0] a, b,
    input cin,
    output [2:0] cout,
    output [2:0] sum );
    
    adder U1(
        .a(a[0])
        ,.b(b[0])
        ,.cin(cin)
        ,.cout(cout[0])
        ,.sum(sum[0])
    );
    adder U2(
        .a(a[1])
        ,.b(b[1])
        ,.cin(cout[0])
        ,.cout(cout[1])
        ,.sum(sum[1])
    );
    adder U3(
        .a(a[2])
        ,.b(b[2])
        ,.cin(cout[1])
        ,.cout(cout[2])
        ,.sum(sum[2])
    );
endmodule

module adder( 
    input a, b, cin,
    output cout, sum );
    assign{cout,sum} = a + b + cin;
endmodule

这道题在文件中需要自己定义一个全加器，因为题目中没有给出现成的全加器模块。

Problem 68 : Adder (Exams/m2014 q4j)

牛刀小试

实现下图中的电路，嗯，随便你用什么方式。此题是一个 4-bit 全加器，与上一题性质相同，但没有上一题中的限制。

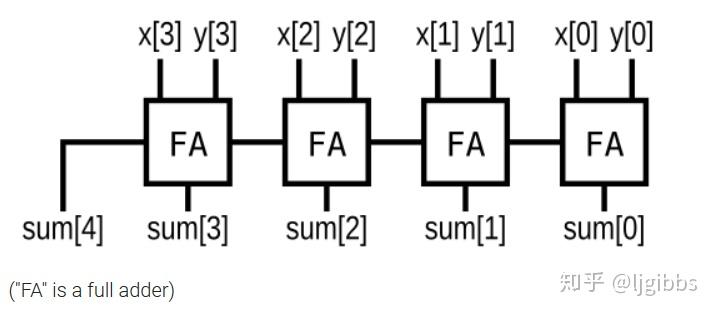
解答与分析

module top_module (
    input [3:0] x,
    input [3:0] y,
    output [4:0] sum
);

    // This circuit is a 4-bit ripple-carry adder with carry-out.
    assign sum = x+y;    // Verilog addition automatically produces the carry-out bit.

    // Verilog quirk: Even though the value of (x+y) includes the carry-out, (x+y) is still considered to be a 4-bit number (The max width of the two operands).
    // This is correct:
    // assign sum = (x+y);
    // But this is incorrect:
    // assign sum = {x+y};    // Concatenation operator: This discards the carry-out
endmodule

既然没有限制，那么 assign sum = x+y; 自然可以。verilog 的语法会自动将 x+y 扩展成 5 bit 数，如果 x+y 产生了进位。但有一点，如果使用位连接符 {x+y},那么结果就会被限制为 4 bit 数。作者觉得这是 Verilog 语法的一个 quirk （怪异之处）。

Problem 69 : Signed addition overflow (Exams/ece241 2014 q1c)

牛刀小试

本题讨论的是有符号数相加的溢出问题中，需要实现一个 2 进制 8bit 有符号数加法器，加法器将输入的两个 8bit数补码相加，产生相加之和以及进位。

解答与分析

module top_module (
    input [7:0] a,
    input [7:0] b,
    output [7:0] s,
    output overflow
); //
 
    assign s = a + b;
    assign overflow = ( a[7] && b[7] && ~s[7] ) || (~a[7] && ~b[7] && s[7]);
    
endmodule

这里从溢出发生的情形出发解题，有符号数溢出有两种情况：一是正正相加，产生正溢出;另一种情况是负负相减，产生负溢出。所以就分别考虑了这两种情况，将这两种情况取或判断溢出。

a[7] && b[7] && ~s[7]：

负数相减（补码相加）产生正数，判断溢出。

~a[7] && ~b[7] && s[7]：

正数相加产生一个负数，判断溢出。

HDLBits：在线学习 Verilog （十四 · Problem 65-69）

Problem 65 : Half adder (Hadd)

Problem 66 : Full adder (Fadd)

Problem 67 : 3-bit binary adder(Adder3 )

Problem 68 : Adder (Exams/m2014 q4j)

Problem 69 : Signed addition overflow (Exams/ece241 2014 q1c)

推荐阅读

推荐阅读

目录