转载自:知乎
首先附上传送门:
Problem 70 100-bit binary adder
题目要求我们创建一个100bit的二进制的加法器,该电路共包含两个100bit的输入和一个cin, 输出产生sum和cout。
(本次练习期望仅使用三行语句),很明显这句话被我无视了。
本题和之前需要用generate语句的题目很类似,但是这样写我觉得确实有点麻烦,评论区如果有好的代码请大家留言。
Hint
这里有好多全加器需要例化,所以采用行为级语句比较好一点。
module top_module(
input [99:0] a, b,
input cin,
output cout,
output [99:0] sum );
wire [99:0] cout_temp;
//这还是将本次计算的cout当作下次计算的cin来使用
fadd inst1_fadd(
.a(a[0]),
.b(b[0]),
.cin(cin),
.cout(cout_temp[0]),
.sum(sum[0])
);
genvar i;
generate
for(i=1; i<100; i=i+1)
begin: add
//例化100次全加器
fadd inst2_fadd(
.a(a[i]),
.b(b[i]),
.cin(cout_temp[i-1]),
.cout(cout_temp[i]),
.sum(sum[i])
);
end
endgenerate
assign cout = cout_temp[99];
endmodule
module fadd (
input a, b, cin,
output sum, cout
);
assign {cout, sum} = a + b + cin;
//assign sum = a ^ b ^ cin;
// assign cout = a&b | a&cin | b&cin;
endmodule
Problem 71 4-digit BCD adder
在本题中,题目给我们提供了一个BCD加法器名字为bcd\_fadd, 输入为两个4bitBCD码,一个cin,产生输出为sum和cout。
module bcd_fadd {
input [3:0] a,
input [3:0] b,
input cin,
output cout,
output [3:0] sum );
且题目也说明需要我们例化4次bcd\_fadd来得到一个4-digit的BCD加法器(共16bit), 同样产生sum和cout。
本题还是在考察我们例化的语法。
module top_module(
input [15:0] a, b,
input cin,
output cout,
output [15:0] sum );
wire [3:0] cout_temp;
//例化4次,注意前一次计算的cout为后一次计算的cin
bcd_fadd inst1_bcd_fadd(
.a(a[3:0]),
.b(b[3:0]),
.cin(cin),
.cout(cout_temp[0]),
.sum(sum[3:0])
);
bcd_fadd inst2_bcd_fadd(
.a(a[7:4]),
.b(b[7:4]),
.cin(cout_temp[0]),
.cout(cout_temp[1]),
.sum(sum[7:4])
);
bcd_fadd inst3_bcd_fadd(
.a(a[11:8]),
.b(b[11:8]),
.cin(cout_temp[1]),
.cout(cout_temp[2]),
.sum(sum[11:8])
);
bcd_fadd inst4_bcd_fadd(
.a(a[15:12]),
.b(b[15:12]),
.cin(cout_temp[2]),
.cout(cout_temp[3]),
.sum(sum[15:12])
);
assign cout = cout_temp[3];
endmodule
Problem 72 3-variable
根据卡诺题来实现电路:
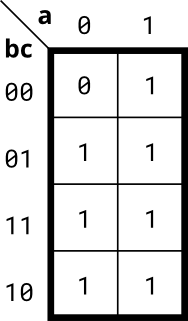
我们可以尝试最大项之积和最小项之和的形式来完成电路设计。
本题很简单
module top_module(
input a,
input b,
input c,
output out );
assign out = a | b | c;
endmodule
Problem 73 4-variable
还是根据卡诺图来设计电路,本题为4个变量。
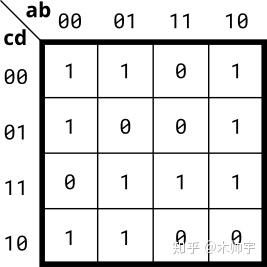
在编写verilog之前,我们可先化简卡诺图。本题我是采用sop(最小项之和),大家也可以尝试一下pos(最大项之积)。
上一题我偷了个懒,看出来就是个or门,这个不行了。
什么是最小项?
最小项: 一个真值表定义一个布尔函数,一个布尔函数可以用乘积项的逻辑和来表示,对应这些乘积项函数的值为逻辑1。如果所有的变量都以原变量或反变量的形式出现,且仅出现一次,这样的乘积项叫做最小项(minterm)。
拿上图举例就是:
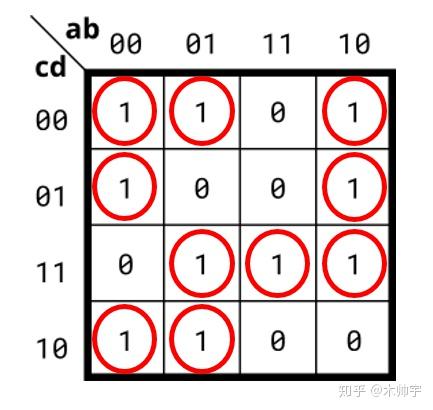
一个布尔函数可以由真值表中所有使函数值为1的最小项的逻辑和来表示,这样的表达式叫做最小项之和(sum of minterm),如图中红圈所示;
解答与解析:
module top_module(
input a,
input b,
input c,
input d,
output out );
assign out = ~b&~c | ~a&~d | a&c&d | ~a&b&c; //化简后的
endmodule
Problem 74 4-variable
根据卡诺图试下如下电路:
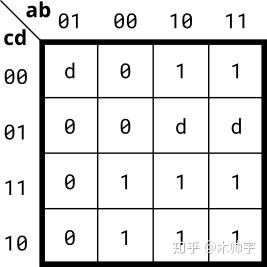
还是先化简卡诺图,其中D为don't care值。相当于X。可以一起圈。
具体可参考:
https://wenku.baidu.com/view/cf5b6748f7ec4afe04a1dfa1.html
可以这样圈:
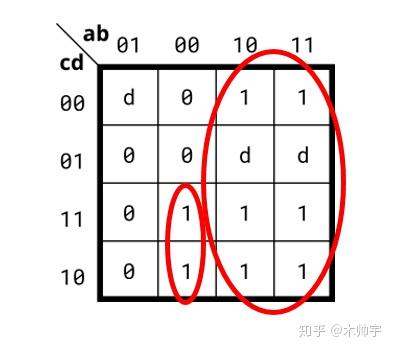
解答与解析:
module top_module(
input a,
input b,
input c,
input d,
output out );
assign out = a | (~a&~b&c);
endmodule
推荐阅读
- HDLBits:在线学习 Verilog (十四 · Problem 65-69)
- HDLBits:在线学习 Verilog (十三 · Problem 60-64)
- HDLBits:在线学习 Verilog (十二 · Problem 55 - 59)
- HDLBits:在线学习 Verilog (十一 · Problem 50 - 54)
关注此系列,请关注专栏FPGA的逻辑


