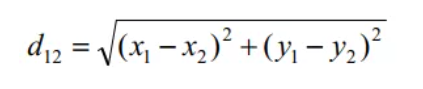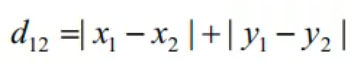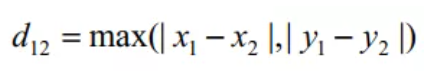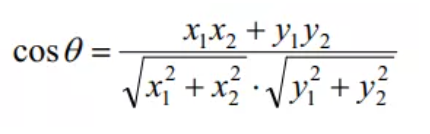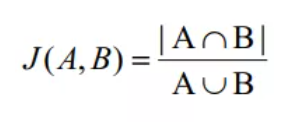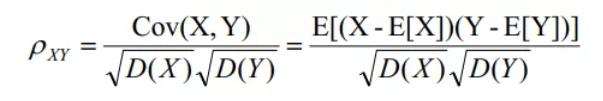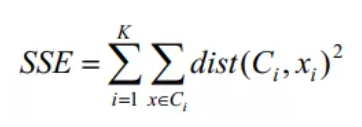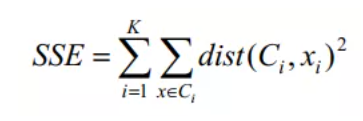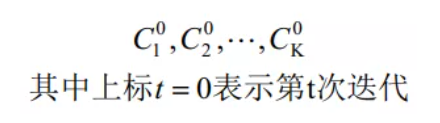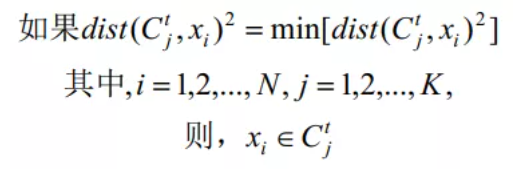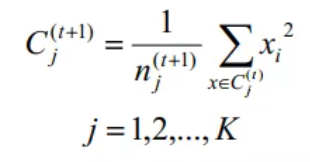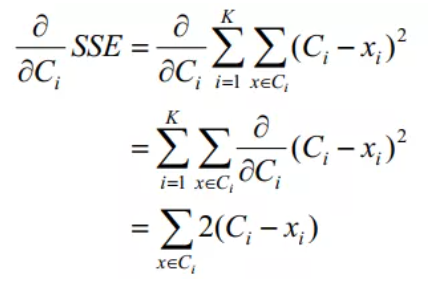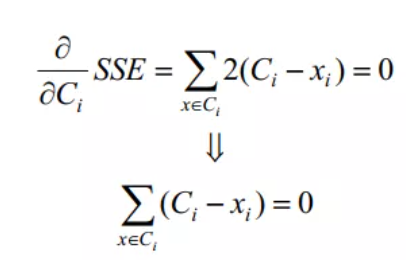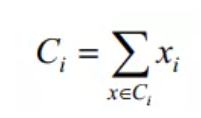简介
K-Means算法是一种基于样本间相似性度量的据类算法,即将数据点到原型的某种距离作为优化的目标函数。
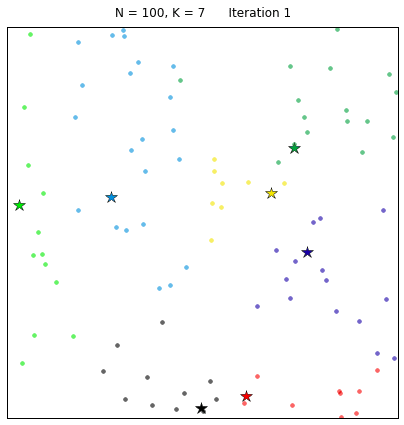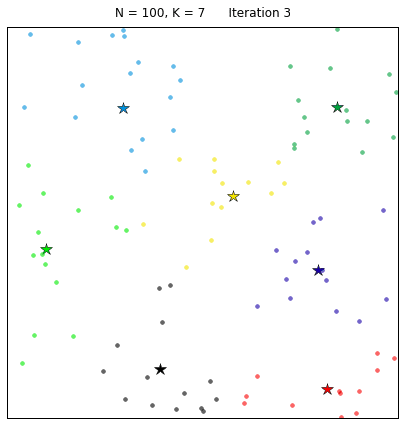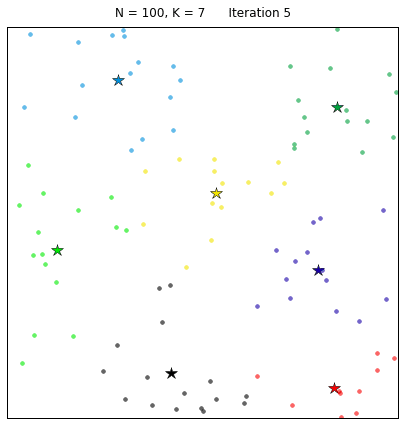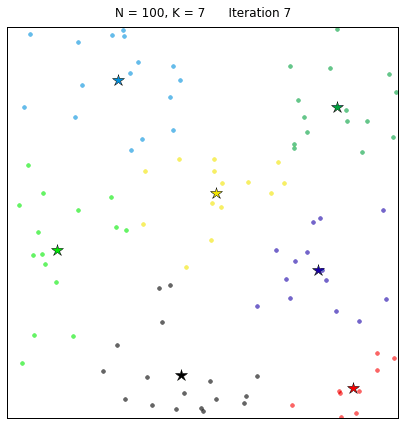
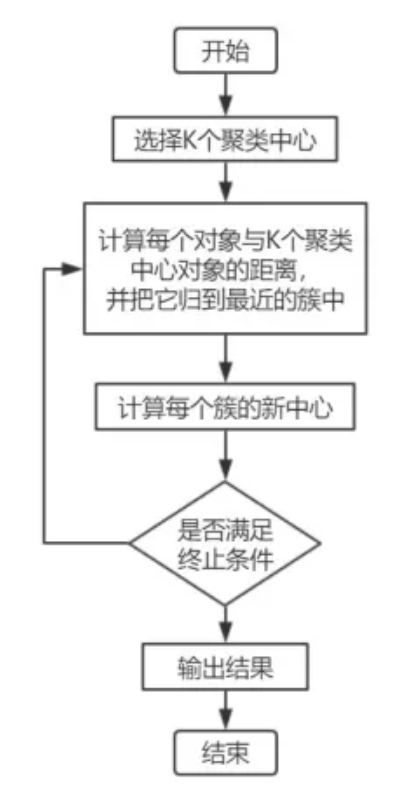
K-Means算法聚类过程示意图
算法的流程
距离度量
1、欧式距离
2、曼哈顿距离
3、切比雪夫距离
4、余弦距离
5、Jaccard相关系数
6、相关系数
而K-Means算法选择的距离度量方法是误差平方和(SSE,Sum of the Square Error),也就是欧式距离,作为聚类的目标函数。该算法的最终目的式得到紧凑且独立的簇。因此两次运行K-Means算法产生两个不同的簇类中,SSE小的那个簇类更优:
其中K表示聚类中心的个数,Ci表示第几个聚类中心,dist表示欧式距离聚类,xi是划分到Ci中的样本。
算法具体步骤的推导
将N个样本{x1,x2,...,xN}划分到K个类{C1,C2,...,CK}中,最小化目标函数:
其中K表示聚类中心的个数,Ci表示第几个聚类中心,dist表示欧式距离聚类,xi是划分到Ci中的样本。
(1) 、从N个数据对象选择K个对象作为初始的聚类中心,记作:
(2)、对待分类的模式特征向量集{xi}中的模式逐个按照最小距离原则划分给K类的某一类,即:
(3)、重新计算每个聚类簇得均值
(4)、循环(2)、(3),直到每个聚类不再发生变化为止,即:
K-Means的灵魂之问
1、为什么要求取簇中各点的均值呢?
对于K个质心求解,最小化目标函数,即对SSE求导并令其等于0,然后求解Cj,即:
在这里令SSE的导数为0,可以得到极值或者最小值(因为欧式距离是凸函数,这也是为什么选择欧式距离的部分原因):
于是可以得到如下的最优解结果:
因此簇最小化SSE的最佳质心在簇中各点的均值位置。
2、初始聚类中心该如何选择呢?
(1)凭经验;
(2)将数据随机分成K类,计算每类中心作为初始聚类中心;
(3)求每个特征点的球心,某一正数r的半径的球形区域中的特征点个数(即该特征的密度),选取密度最大的特征点为第一个初始聚类中心,然后再该中心大于距离d的那些特征点中选取另一个具有最大密度得特征点作为第二个聚类中心,直到选取K个初始聚类中心;
(4)用相距最远的特征点作为聚类中心;
(5)当n较大时,先随机地从n个模式中取出一部分模式用层次聚类的方法聚类成K个类,然后每类的中心作为初始聚类中心。
3、初始聚类中心的个数K该如何抉择呢?
(1)按先验知识进行抉择;
(2)手肘法:让K从小到大逐步增加,每个K都会用K-Means算法分类。目标函数随着K的增加而单调减少,但速度在一定的程度上会减少,曲率变化最大的那个点对应最优的聚类数K。
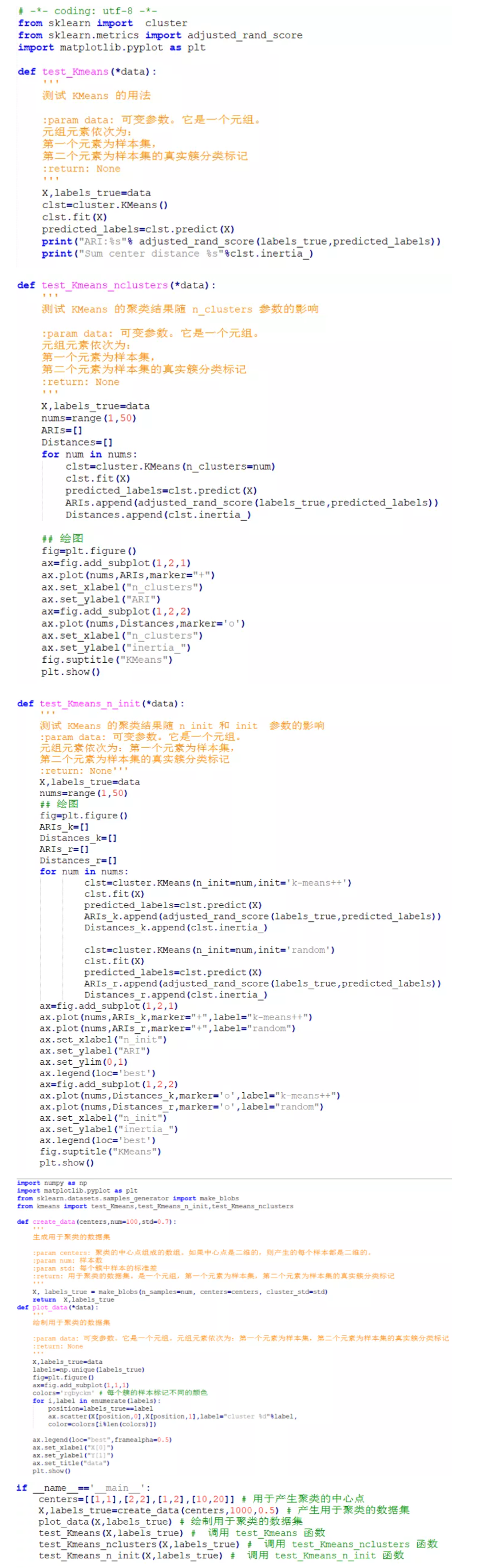
K-Means算法的实践
K-Means算法实践
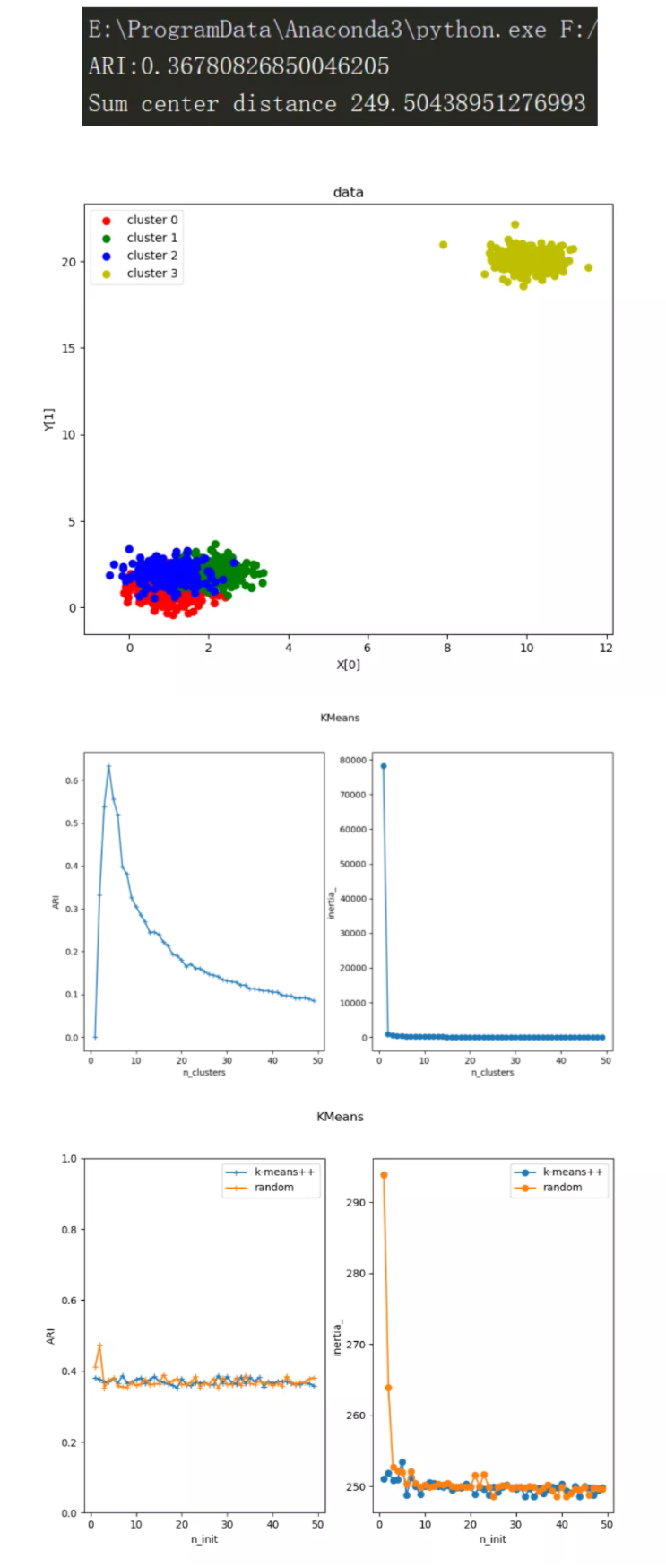
执行结果:
文章转载于:集智书童
作者:ChaucerG
推荐阅读
更多嵌入式AI技术相关内容请关注嵌入式AI专栏。