M1 Max初相遇，快快乐乐写卷积

作者：高洋
转载链接：https://zhuanlan.zhihu.com/p/464740681

11月份入了M1 Max版本的MBP14，吃了两个月灰，春节终于有时间体验了一下apple silicon的威力~

这颗SoC的能力非常夸张，有4发射SIMD的能力，同时缓存子系统和内存带宽强到了没朋友，只是主频弱了些，只有3.2GHz，矩阵乘法的kernel随便写一写就能99%+峰值。

本篇文章就是介绍一下如何在这颗最现代的CPU上非常简单地实现一下CNN里面的卷积算法，并可以轻松达到90%+的浮点峰值效率~ 全部代码已经开源到
https://github.com/pigirons/conv3x3_m1

测试浮点峰值

老规矩，新的架构要测一下峰值性能才能清楚最终优化的天花板，arm提供的乘加指令可以支持标量乘向量，即向量a的某条lane乘以向量b的每一个lane，累加到向量c上对应的lane；由于是四发射SIMD，假设每条mla指令延迟4个周期，需要构造16条流水线，所以测试代码如下：

.loop1:
    fmla v0.4s, v16.4s, v17.s[0]
    fmla v1.4s, v16.4s, v17.s[1]
    fmla v2.4s, v16.4s, v17.s[2]
    fmla v3.4s, v16.4s, v17.s[3]
    fmla v4.4s, v16.4s, v17.s[0]
    fmla v5.4s, v16.4s, v17.s[1]
    fmla v6.4s, v16.4s, v17.s[2]
    fmla v7.4s, v16.4s, v17.s[3]
    subs x0, x0, #1
    fmla v8.4s, v16.4s, v17.s[0]
    fmla v9.4s, v16.4s, v17.s[1]
    fmla v10.4s, v16.4s, v17.s[2]
    fmla v11.4s, v16.4s, v17.s[3]
    fmla v12.4s, v16.4s, v17.s[0]
    fmla v13.4s, v16.4s, v17.s[1]
    fmla v14.4s, v16.4s, v17.s[2]
    fmla v15.4s, v16.4s, v17.s[3]
    bne .loop1

每一条fmla指令，都是从v17里取一个标量，乘以v16向量，累加到v0-v15里面，没有数据相关。x0循环1024^3次，测得的峰值如下：

time = 1.351155s, perf = 102.122379 GFLOPS.

前面讲到CPU主频3.2GHz，理论浮点峰值3.24(4+4)=102.4 GFLOPS，已经非常接近。减少fmla指令数量，峰值就会下降，说明单条指令延迟就是4个周期，这里就不贴具体实验过程了。

矩阵乘法kernel实现

CNN中的卷积算法，最通用的一大类实现，就是将多通道的卷积运算，转换成矩阵乘法运算。在早期的深度学习框架比如caffe中，典型的算法是im2col + gemm两个完全分开的独立函数。在gemm中，需要先对大矩阵做分块拷贝，这样可以充分利用缓存降低主内存带宽的压力，以及大幅降低TLB的miss数量。对于大矩阵，引入这个操作的好处远大于成本，但是深度学习遇到的矩阵，往往不是一个平衡的大矩阵，这个操作的成本也许会非常高。所以我们实现卷积的时候，最好在im2col阶段，就直接构造好矩阵乘法kernel需要的格式。这一节我们先介绍在arm上常用的向量外积矩阵乘法kernel。

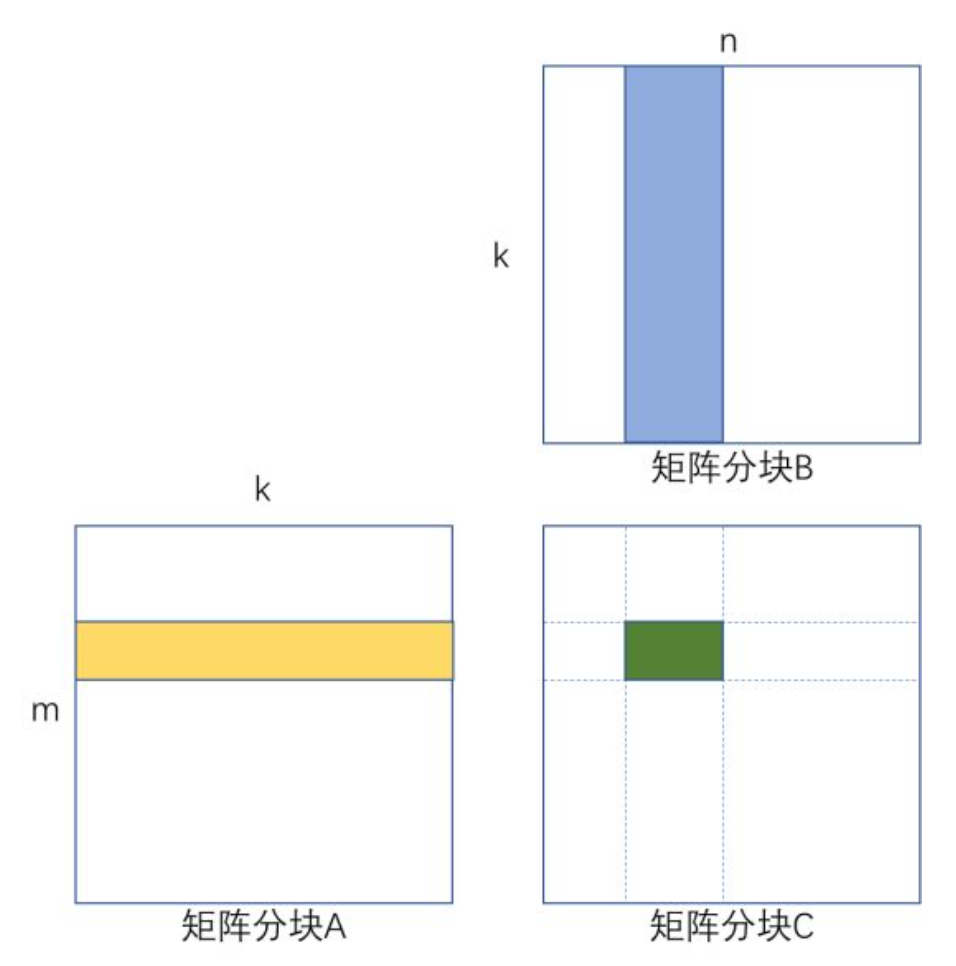
如下图所示，矩阵分块C += A × B，绿色部分表示构造的向量外积寄存器分块，不停读取矩阵分块A中黄色部分的列向量，和矩阵分块B中蓝色部分的行向量，做乘法，并累加到绿色的寄存器分块矩阵内。

矩阵乘法分块kernel示意

根据之前
高洋：关于sgemm_hsw的一点解释说明

这篇文章的介绍，我们尽量构造比较大的寄存器分块，这里可以构造成8×12的分块，需要24个寄存器。

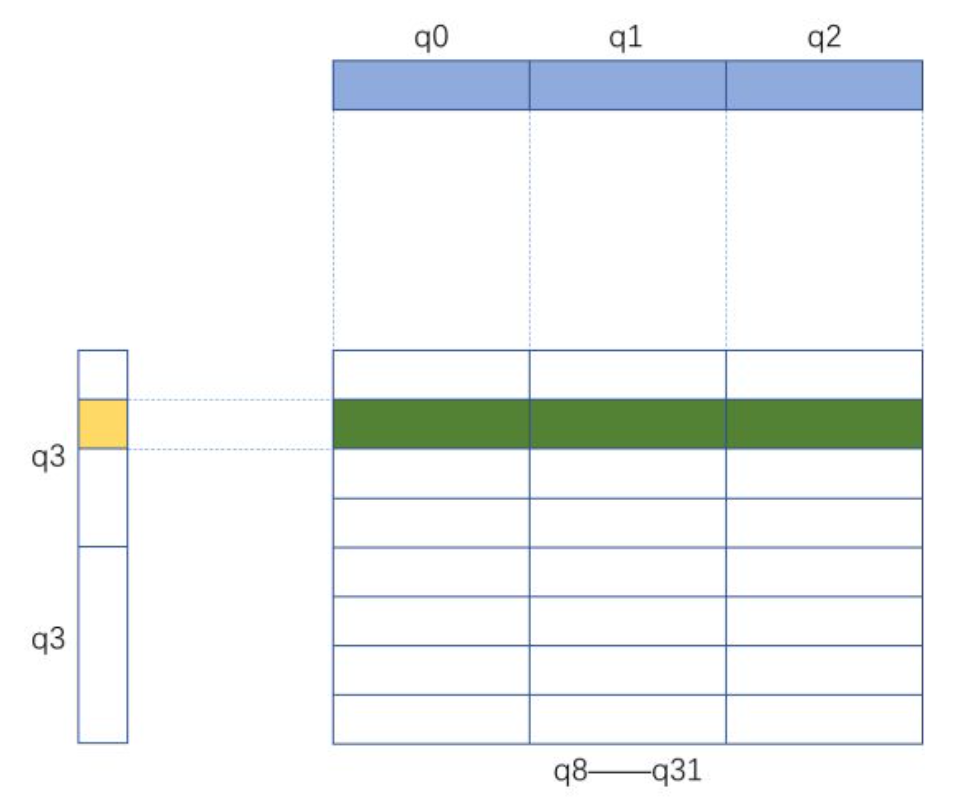
矩阵乘法kernel的寄存器分块示意

如上图所示，q0-q2读取B矩阵的行向量，q3分时读取A矩阵列向量，一组做24个标量乘向量后累加到q8-q31表示的C矩阵寄存器分块。

按照早期arm公版架构设计（Cortex-A73及以前），arm的乱序多发射能力非常有限，需要仔细排布整个kernel每一条指令的计算过程，才能达到接近理论浮点峰值的能力（最高95%左右）。经过测试，M1系列芯片根本不需要如此麻烦，像x86那样直接排布指令就可以达到峰值性能，核心的代码大致如下：

    ldr q0, [x9, #0]
    ldr q1, [x9, #16]
    ldr q2, [x9, #32]
    ldr q3, [x11, #0]
    fmla v8.4s, v0.4s, v3.s[0]
    fmla v9.4s, v1.4s, v3.s[0]
    fmla v10.4s, v2.4s, v3.s[0]
    fmla v11.4s, v0.4s, v3.s[1]
    fmla v12.4s, v1.4s, v3.s[1]
    fmla v13.4s, v2.4s, v3.s[1]
    fmla v14.4s, v0.4s, v3.s[2]
    fmla v15.4s, v1.4s, v3.s[2]
    fmla v16.4s, v2.4s, v3.s[2]
    fmla v17.4s, v0.4s, v3.s[3]
    fmla v18.4s, v1.4s, v3.s[3]
    fmla v19.4s, v2.4s, v3.s[3]
    ldr q3, [x11, #16]
    fmla v20.4s, v0.4s, v3.s[0]
    fmla v21.4s, v1.4s, v3.s[0]
    fmla v22.4s, v2.4s, v3.s[0]
    fmla v23.4s, v0.4s, v3.s[1]
    fmla v24.4s, v1.4s, v3.s[1]
    fmla v25.4s, v2.4s, v3.s[1]
    fmla v26.4s, v0.4s, v3.s[2]
    fmla v27.4s, v1.4s, v3.s[2]
    fmla v28.4s, v2.4s, v3.s[2]
    fmla v29.4s, v0.4s, v3.s[3]
    fmla v30.4s, v1.4s, v3.s[3]
    fmla v31.4s, v2.4s, v3.s[3]

具体的代码参考sgemm_kernel_m1.S，上面这个片段，描述了沿k方向做一次向量外积的实现，实际代码里面我们将k循环展开4次，为了在处理边界情况下，均摊某些偏移计算带来的开销。

为了处理边界，我们设计了m8n12到m4n4等6个函数，分别处理m除以8（余0或4）和n除以12（余0，4或8）的6种不同余数组合。

最后测试一下性能，使用build_sgemm_kernel.sh编译，m设计为8的倍数，n为12的倍数，k为4的倍数且尽量大：

m = 24，n = 24，k = 64，time = 0.734408us，perf = 100.391037 GFLOPS.
m = 48，n = 48，k = 128，time = 5.793055us，perf = 101.815701 GFLOPS.
m = 96，n = 96，k = 256，time = 46.102392us，perf = 102.350264 GFLOPS.
m = 144，n = 144，k = 288，time = 117.041920us，perf = 102.048360 GFLOPS.

可以看到在各种case下性能非常接近，且最高可以做到102.35 GFLOPS（99.95%的理论浮点峰值）。同样的程序在一颗Cortex-A72上测试，只能做到80%不到的峰值，更早期的arm架构效率会更差，apple silicon真·现代处理器之光~ 不过根据之前适配端侧芯片的经验估计，可能最早从Cortex-A75到Cortex-A76这两代开始，arm公版的乱序发射执行能力也上来了，虽然仍然不如苹果的芯片，但是对付这样的sgemm kernel应该问题不大。

一种tile gemm的卷积实现

本节介绍一种针对im2col + gemm标准算法的优化——tile gemm卷积算法。本质就是改造im2col过程的缺陷，使其既有很好的空间局部性，又可以直接生成sgemm kernel需要的矩阵分块格式，减少了标准gemm中的分块步骤。这里为了简单又不失一般性，我们实现filter是3x3，stride是1的卷积，同时Tensor的排布格式使用常用的nchw格式。

sgemm kernel，我们这里选择m = n = 144，k = 288这个case，其中矩阵A（m×k）从filter提取分块；矩阵B（k×n）从input tensor提取分块；矩阵C（m×n）写回output tensor里。

作为推理用的卷积，filter可以事先做好重排处理：

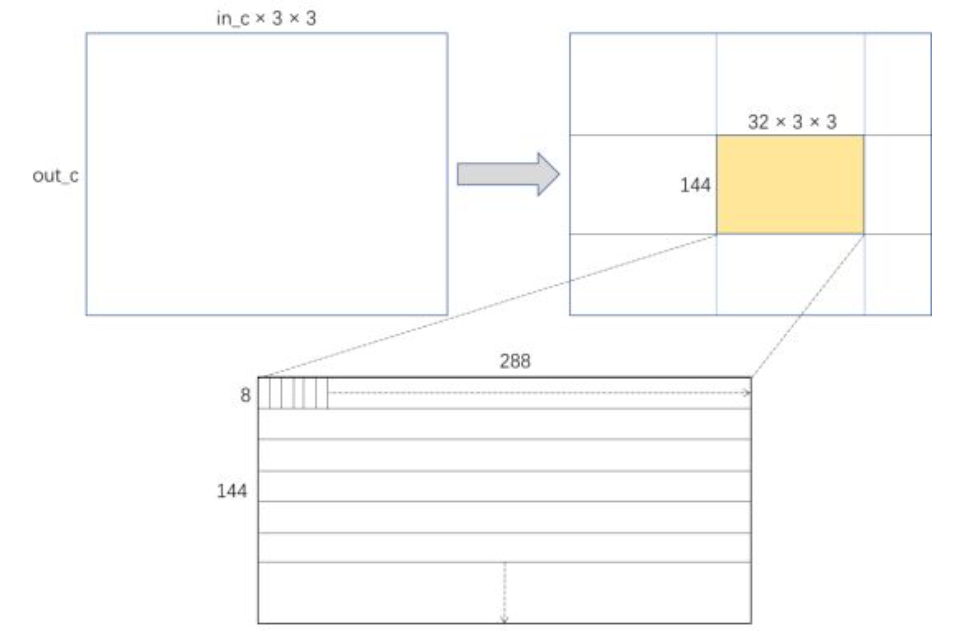
卷积核重排

如上图所示，filter可以表示成一个out_c乘以in_c×3×3的大矩阵，为了适应sgemm kernel的分块大小，可以将这个矩阵分成若干个144×288（32×3×3）的小矩阵。每个小矩阵内部按照sgemm kernel的要求，重排成下边这种从上到下每个8×288的长条矩阵转置后的顺序。

然后是每次卷积内部要对input tensor做分块：

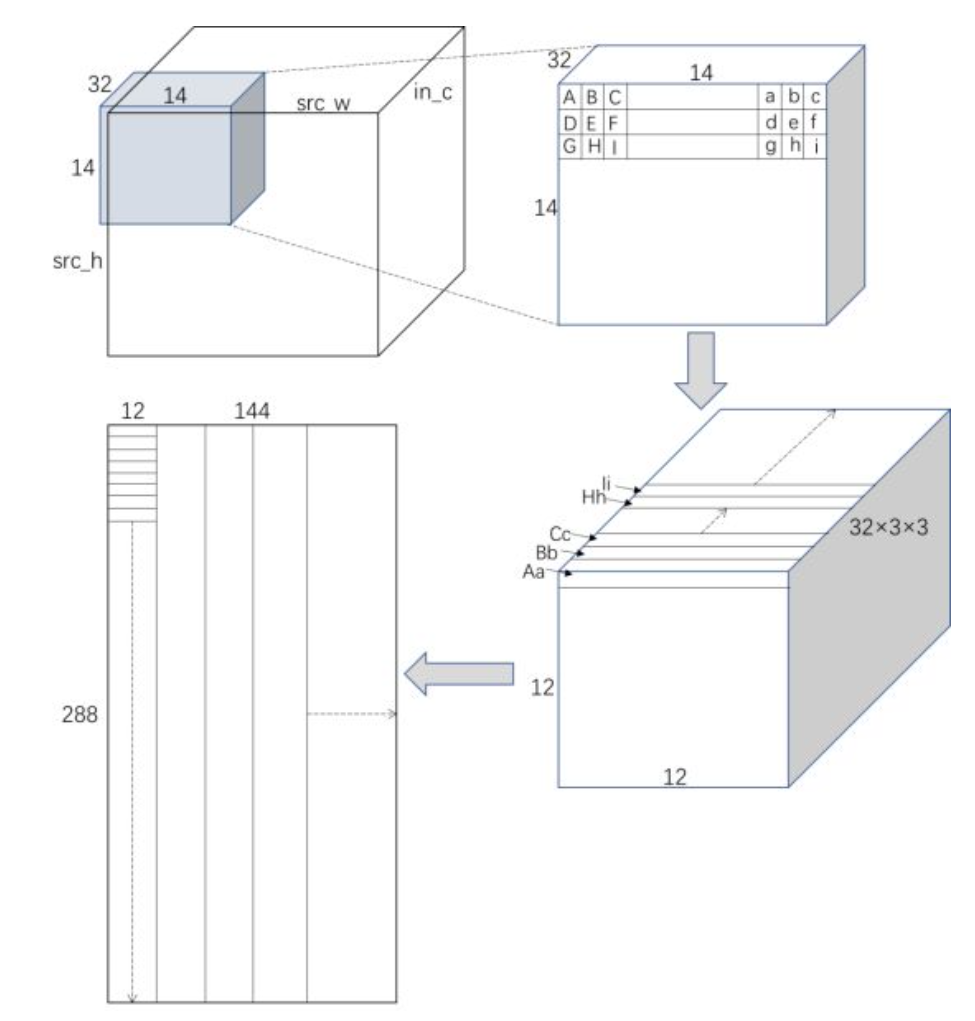
输入Tensor的分块和重排

首先从intput tensor里面分出来一个14×14×32的灰色小分块，注意卷积计算可能有padding，所以图中灰色的小分块是从外面padding处开始的。根据im2col的原理，这个14×14×32的小分块，包含了3×3卷积的复用，展开成矩阵乘的形式，就可以按照右上面这个Tensor中的标注，把向量Aa（即字母A到字母a表示的向量），Bb，Cc...Hh，Ii全部展开，形成右下角这样的Tensor，展开的方向和channel这一维相乘，就变成一个12×12×288（32×3×3）的Tensor，最后把12×12拉平，就变成了sgemm kernel里面的矩阵B分块，即左下角的表示。

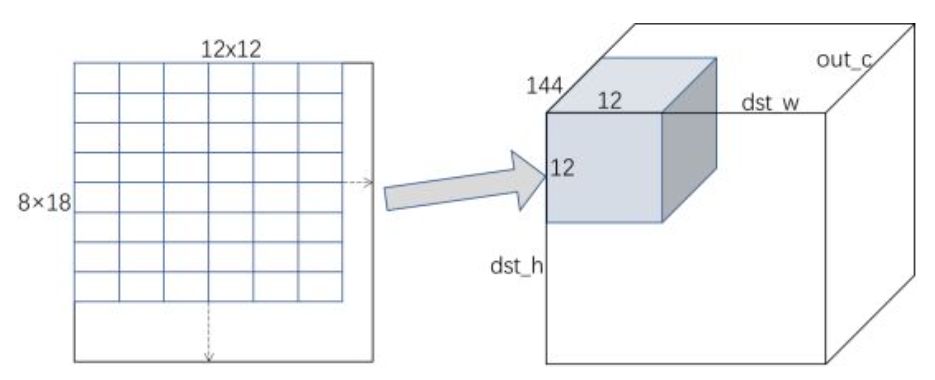
最终两个矩阵分块A和B相乘，得到下图左边这个矩阵C，大小是144（8×18）×144（12×12）。这个矩阵内部是按8×12的寄存器分块排布的，所以最终还需要做一次转换，与bias相加以后，写入output tensor，如下图右边灰色部分所示。

结果矩阵重排并写入输出Tensor

前面描述了一个分块的转换和乘法过程，将所有的分块都做一遍这个过程，就完成了卷积的运算。做的顺序应该先沿input_channel维度，再沿Tensor的w和h维度，不断滑动，直至遍历完成。

最后我们以VGG16中的典型卷积参数做一个测试：

conv = 224×224×64×64，padding = 1，time = 41.229ms，perf = 89.727447 GFLOPS
conv = 112×112×128×128，padding = 1，time = 38.909ms，perf = 95.078781 GFLOPS
conv = 56×56×256×256，padding = 1，time = 37.752ms，perf = 97.991805 GFLOPS
conv = 28×28×512×512，padding = 1，time = 37.471ms，perf = 98.725626 GFLOPS
conv = 14×14×512×512，padding = 1，time = 9.666ms，perf = 95.679393 GFLOPS

按照之前计算的浮点峰值102.4 GFLOPS算，大多数可以达到92%以上的浮点峰值，最高可以达到96%... Apple Silicon YYDS~

后记

苹果的M1系列芯片为业界带来了新的生产力增长点，让我们看到了在x86之外，还有更多更好的选择。自研架构相对公版架构，也表现出了非同寻常的定制能力。未来几年，在云服务器，桌面和移动生产力领域，arm作为搅局者将给这些场景带来新的活力。作为软件开发者，新的芯片技术可以使我们更轻松高效地实现高性能软件和系统，更快地完善生态的建设。

真是有点期待Mac Pro的终极版Apple Silicon啊...

最后还是广告时间，OpenPPL在年前已经支持了对目前业界主流的arm server处理器的支持，除了公版架构，还有国产的泰山核和飞腾服务器~ 开源地址：
https://github.com/openppl-public

推荐阅读

更多嵌入式AI技术相关内容请关注嵌入式AI专栏。

测试浮点峰值

矩阵乘法kernel实现

一种tile gemm的卷积实现

更多技术问题

后记

推荐阅读

目录