HCI与NBTI一争天下
晶体管的老化效应主要是HCI与NBTI已经是无需争论的事实,而HCI在电路中主要受到信号翻转率(SA,Switch Activity)的影响,而NBTI主要受到信号占空比(SP,Signal Probability)的影响也早已成为常识,并在多篇问论文中体现[1][2]。集成电路的老化或者说这里的晶体管的老化会同时存在这两种效应,但是如果这两种效应的占比不同则会影响后续对老化的监控与缓和策略,因此第一步需要搞清楚晶体管中HCI与NBTI这两种老化效应的占比关系。
在2009年的论文[3]中,就讨论了这样一个问题。首先HCI可以分为NMOS内的HCI效应,即NHCI以及PMOS内的HCI效应即PHCI,但是NBTI只存在与PMOS内,NMOS内的BTI常常被忽视。这篇论文第一步就仿真出了晶体管级的NHCI PHCI以及NBTI效应造成的饱和漏电流的退化,如下图。其中,NBTI导致的饱和漏电路的退化至少小于HCI导致的退化10倍,同时得到了其饱和漏电流的退化模型。
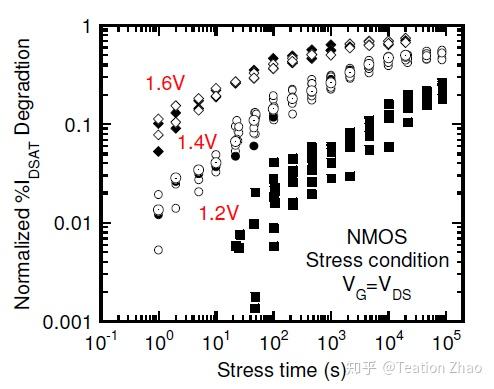
HCI导致的NMOS饱和漏电流退化
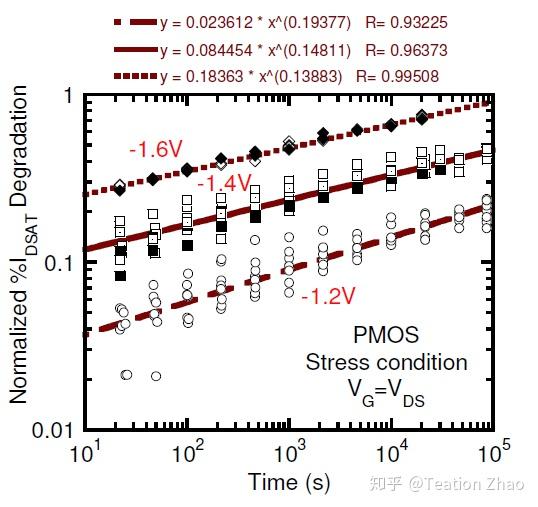
HCI导致的PMOS饱和漏电流退化
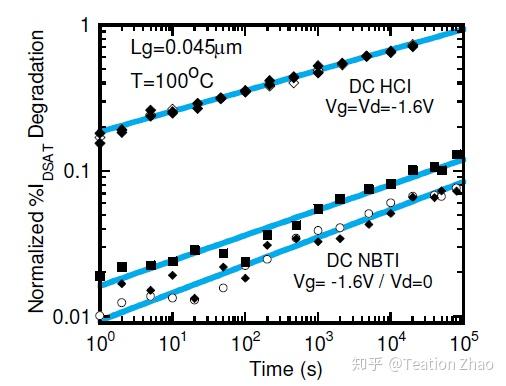
HCI与NBTI导致的PMOS饱和漏电流退化
接着论文又在电路级进行了仿真,搭建了一个环形振荡器。首先,环形振荡器的震荡频率与电路延迟的关系是:
其中 为反相器延迟, 为震荡频率, 是NMOS的导通延迟, 则是PMOS的导通延迟。反相器从0变1的延迟时间可以认为是PMOS的导通延迟,而反相器从1变0的延迟时间则可以认为是NMOS的导通延迟,那么反向器的平均延迟就是NMOS与PMOS导通延迟的平均数。进一步地,导通延迟在电源电压 与栅电容不变的条件下,导通延迟与漏电流成反比。那么可以进一步地得到振荡器频率与漏电流了关系,带入前面得到的漏电路退化模型,那么就可以使用振荡器频率的退化来表征各个效应带来的漏电流的退化,也就是各个老化效应的强度。
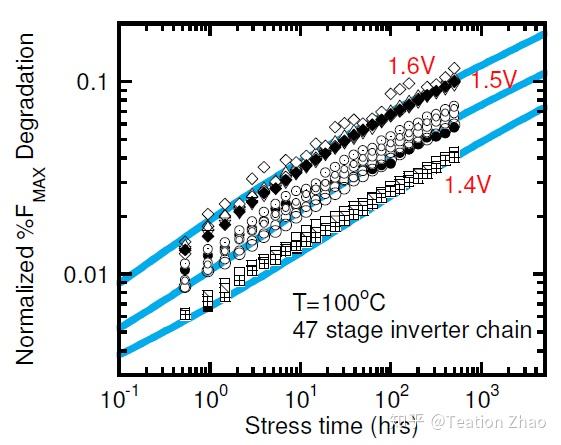
RO震荡频率退化
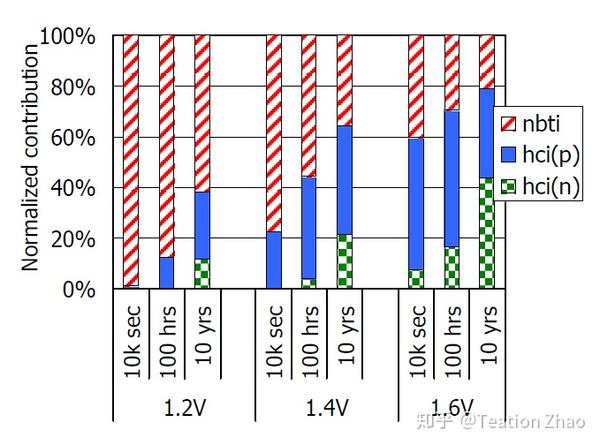
各种效应在不同时间与电压的占比
第一个图是振荡频率在不同电压下的退化图,而第二个则是HCI与NBTI在电路老化中的占比,可见,无论电压是多少,随着时间的增加,HCI造成的老化在总体老化中的占比会越来越大。因此可以得出结论是在1.6V电压下,电路老化的前期关键因素是NBTI而后期的关键因素则是HCI。但是在1.2V电压下,即使10yrs时,HCI老化的占比也没有超过40%,同时由于在真实电路中,信号翻转率并不是很高,环形振荡器模型其实也放大了HCI效应。也就是说,随着晶体管特征尺寸的继续缩小,电压的继续下降,NBTI老化效应带来的影响永远都是在电路老化中占有绝对的比重。
NBTI的终极目标
既然知道了NBTI在晶体管老化过程中占有最大的比重,那么接下来的问题就是NBTI到底会造成什么样的影响,对NBTI的监测的终极目标是什么。NBTI最终一定会造成晶体管的失效,但是在真实时间尺度下想要单纯的使晶体管由于NBTI而失效几乎是无法完成的使命。
在一篇2005年的论文[4]中,为对器件寿命进行估计,使用的是阈值电压偏移10%作为寿命终点。
Currently there is no clear specification for the characterization of the NBTI lifetime across industry.
A reasonable failure criterion for the 90nm CMOS technology is, for instance, to tolerate a maximum shift of 10% for the key device parameters VT and IDsat at 125 C.
在三星电子2014年的论文[5]中,同样使用这种方法来仿真器件的寿命,只是他们将VT偏移界限设置在了20%。
即便是加速寿命实验(高温高压)的条件下,经过2000小时也只能达到10%左右的延迟增加[6],也就是说NBTI效应虽然会造成器件的最终失效,但是几乎无法观测到。那么可以得出的结论是:对于NBTI效应的影响,应该主要关注其带来的延迟提升进而造成的时序问题。
芯片中不只有晶体管
在一篇更古老的1995年的论文[7]里面,对集成电路中金属互连线的EM与SM效应进行了实验分析,得到的结论是:电流冲击次数会造成互连线特征参数成指数级的退化,电流密度会使平均失效时间成指数级的下降。电流密度可以由工艺提升得到缓解,而电路冲击次数,即栅电容的充放电次数则与信号的翻转率相关。
总的来看
在论文[8]里面对这些效应有一个横向的对比,虽然这篇论文的核心是介绍他们的老化预警机制,但里面介绍部分的分析却提供了很多信息。首先是这篇文章引用了[9]两个公式,分别是:
表示阈值电压在HCI老化机制下正比于老化时间的n次幂,这里的 在0.45左右
表示阈值电压在NBTI老化机制化正比于时间乘以压力系数的 次幂,这里的 在0.16-0.25之间, 表示压力系数,由于前面提到的NBTI在电路中主要受到SP的影响,即晶体管打开时间的占比,即为 。
在第二节介绍的论文里面可以说是在横向对比HCI与NBTI两种老化机制的差异,而简化了或者忽略了这些机制间的纵向对比,即不同时间尺度下的对比。同时这里这篇论文还引入了一些其他的老化机制。利用其幂函数性质因此得出了这么一个图:
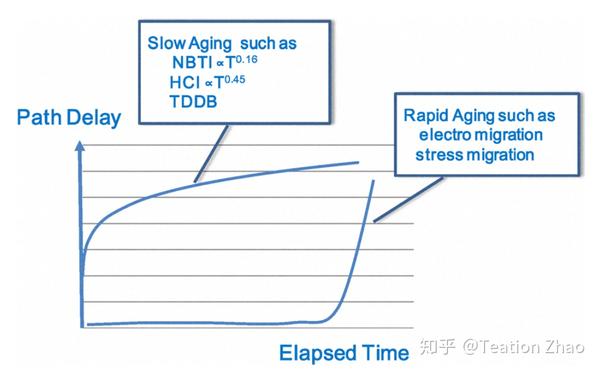
多种老化效应对比
引入EM和TDDB,这个图说明HCI与NBTI在短时间内造成延迟急剧上升,但是一定时间后会放缓,电路中的表现为电路延迟急剧上升,然后减缓,最终在某个时刻器件失效。但是EM和SM确实另一种表现,这两种下效应在短时间内可以说毫无表现,但会在突然某个时刻爆发失效。
结论
通过总结这些论文,从短时间与长时间两个方向得出结论:
短时间
可能需要注意NBTI效应带来的电路延迟增加,进而导致的一些时序问题。解决时序问题就有很多手段:
- 在设计阶段使用Aging-Aware时序分析预留更多的时序余量
- 使用On-Time Sensor的监测结果来限制DFS的最大频率
长时间
在芯片生命周期的后期,造成芯片失效的原因更可能是EM/SM效应,所以也需要特定的电路来实现对其的监测与缓和。
参考
- ^D. Sengupta and S. S. Sapatnekar, "Estimating Circuit Aging Due to BTI and HCI Using Ring-Oscillator-Based Sensors," in IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 36, no. 10, pp. 1688-1701, Oct. 2017.
- ^A. Amouri, F. Bruguier, S. Kiamehr, P. Benoit, L. Torres and M. Tahoori, "Aging effects in FPGAs: an experimental analysis," 2014 24th International Conference on Field Programmable Logic and Applications (FPL), Munich, 2014, pp. 1-4.
- ^T. Nigam, "Impact of Transistor Level degradation on product reliability," 2009 IEEE Custom Integrated Circuits Conference, Rome, 2009, pp. 431-438.
- ^R. Wittmann, H. Puchner, L. Hinh, H. Ceric, A. Gehring and S. Selberherr, "Impact of NBTI-driven parameter degradation on lifetime of a 90nm p-MOSFET," 2005 IEEE International Integrated Reliability Workshop, S. Lake Tahoe, CA, 2005, pp. 4 pp.-.
- ^M. Park, G. Yang, J. Yang, K. Lee and Y. Park, "New perspective on lifetime prediction approach for BTI and HCI stressed device and its impact on circuit lifetime," 2014 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Yokohama, 2014, pp. 337-340.
- ^Edward A. Stott, Justin S.J. Wong, Pete Sedcole, and Peter Y.K. Cheung.” Degradation in FPGAs: measurement and modelling.” In Proceedings of the 18th annual ACM/SIGDA international symposium on Field programmable gate arrays (FPGA ’10). Association for Computing Machinery, New York, NY, USA, 229–238.
- ^T. Takewaki, H. Yamada, T. Shibata, T. Ohmi and T. Nitta, "Excellent electro/stress-migration-resistance giant-grain copper interconnect technology for high-performance power devices," Proceedings of International Symposium on Power Semiconductor Devices and IC's: ISPSD '95, Yokohama, Japan, 1995, pp. 438-442.
- ^Y. Sato et al., "A circuit failure prediction mechanism (DART) for high field reliability," 2009 IEEE 8th International Conference on ASIC, Changsha, Hunan, 2009, pp. 581-584.
- ^W. Wang, V. Reddy, A. T. Krishnan, R. Vattikonda, S. Krishnan and Y. Cao, "Compact Modeling and Simulation of Circuit Reliability for 65-nm CMOS Technology," in IEEE Transactions on Device and Materials Reliability, vol. 7, no. 4, pp. 509-517, Dec. 2007.
END
知乎:https://zhuanlan.zhihu.com/p/114212933
推荐阅读
更多内容请关注其实我是老莫的网络书场专栏


