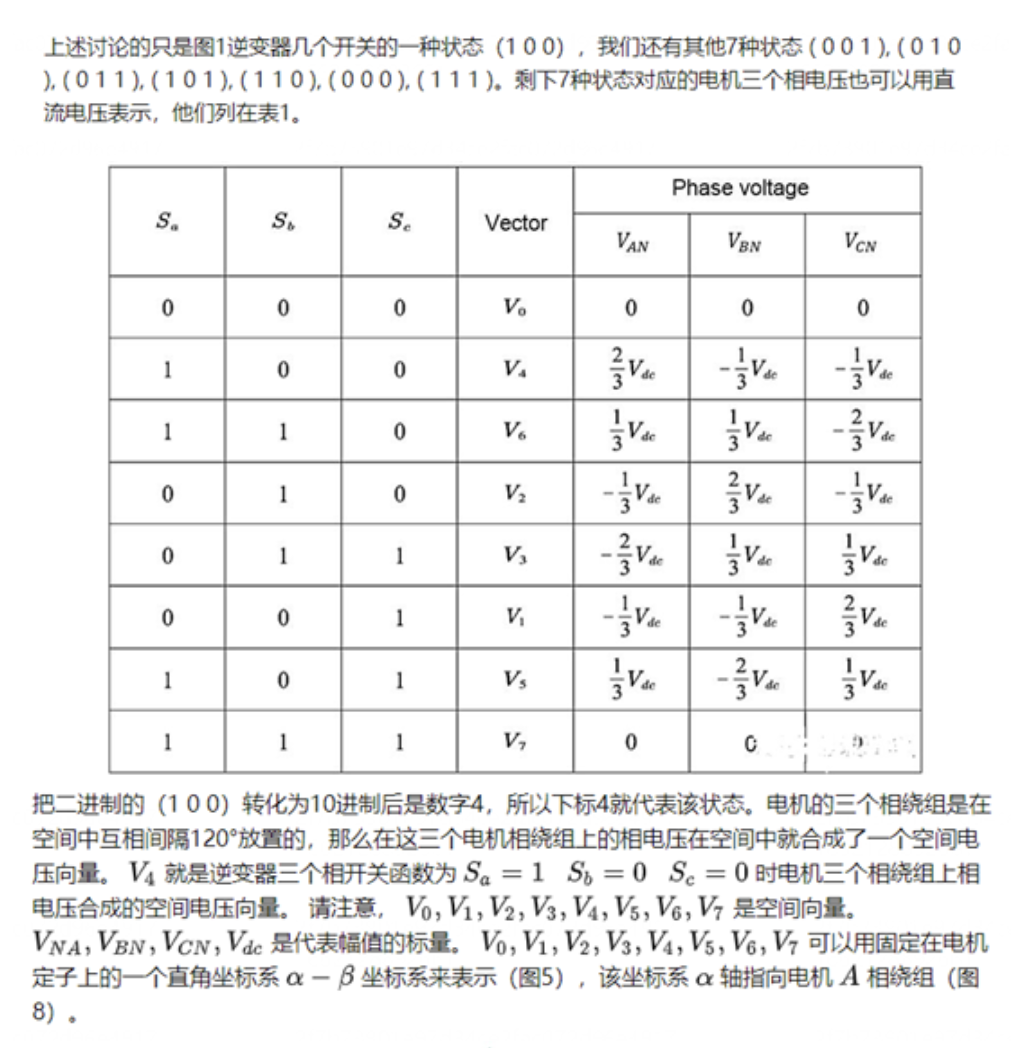
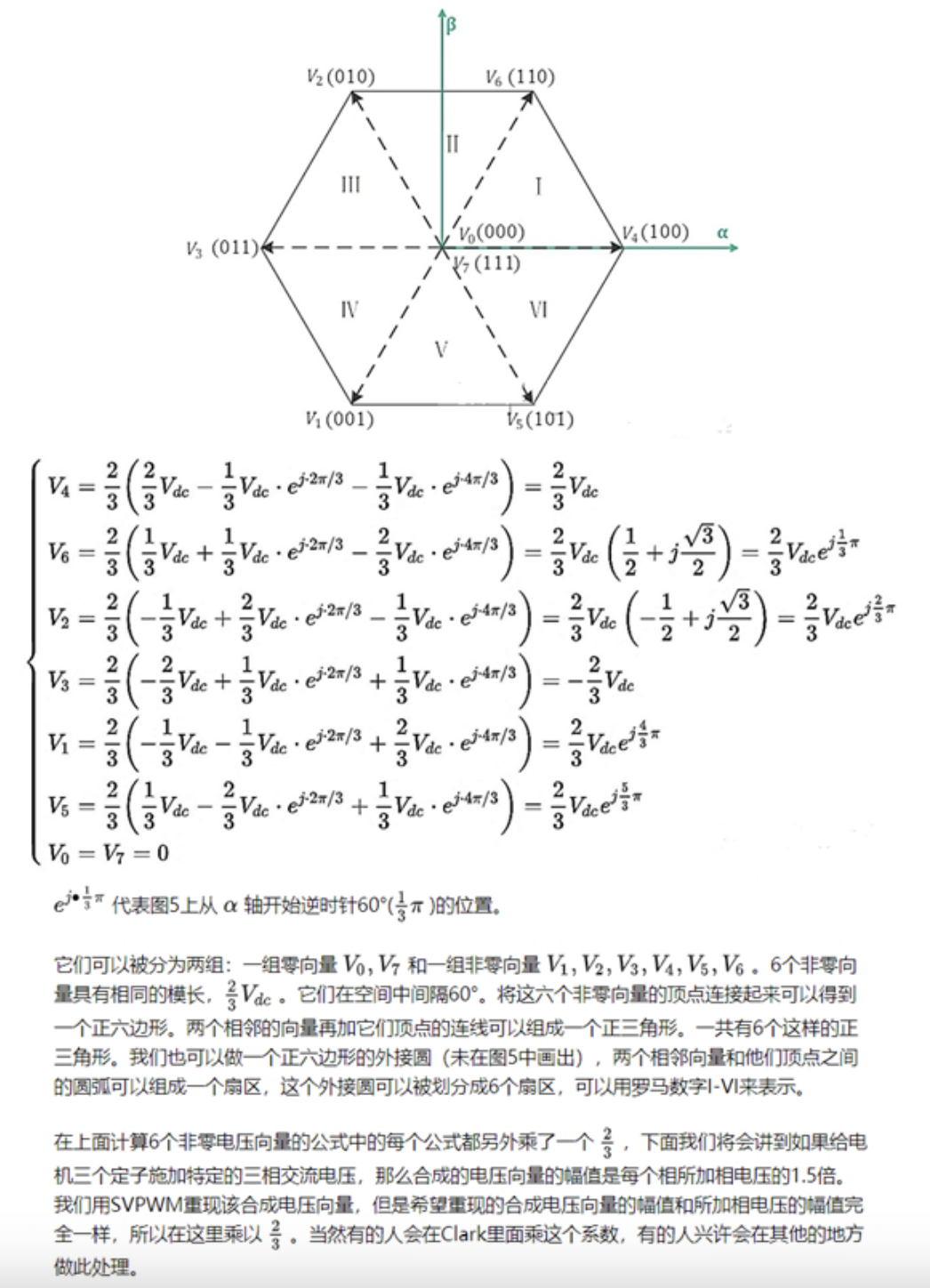
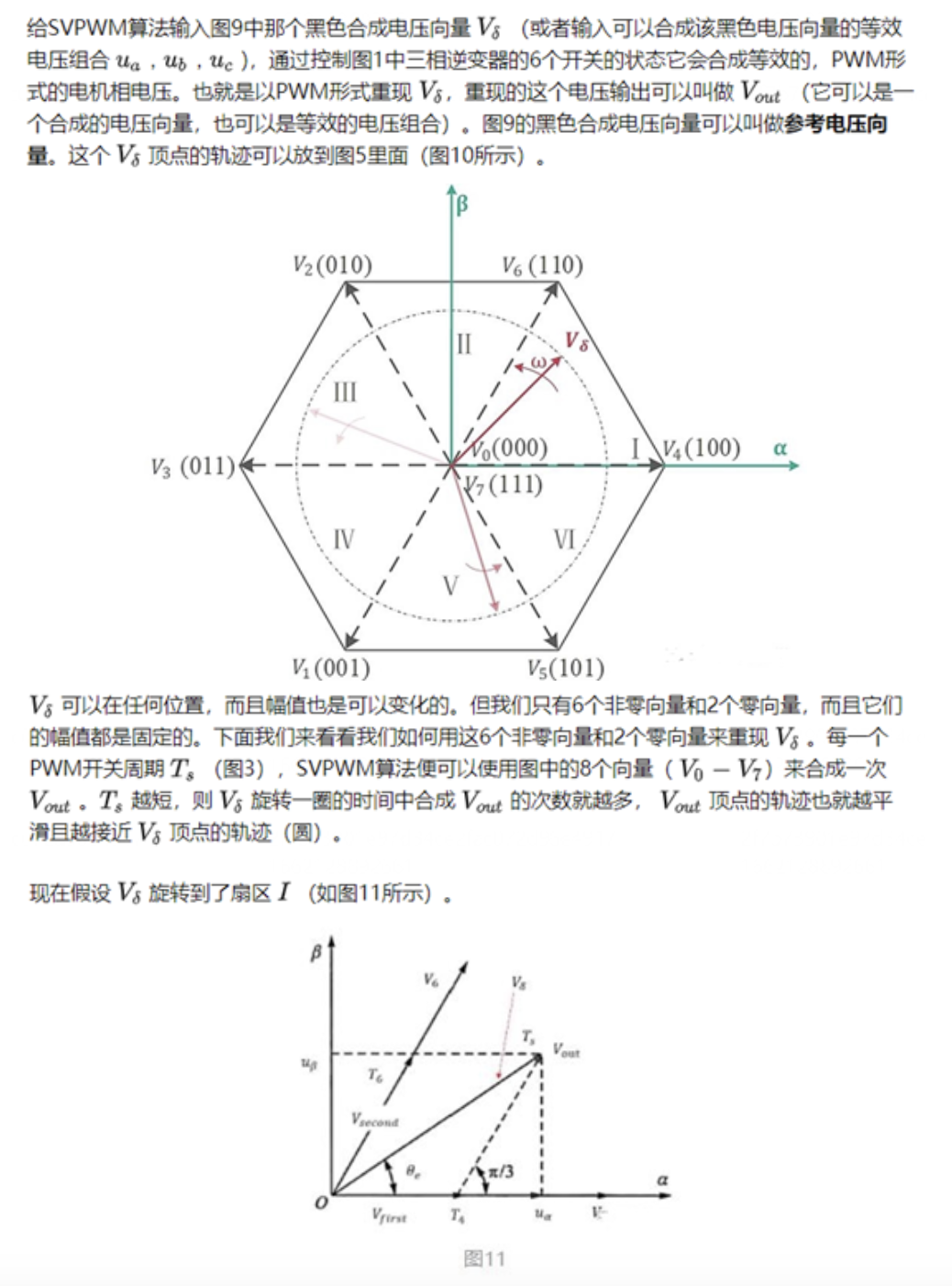
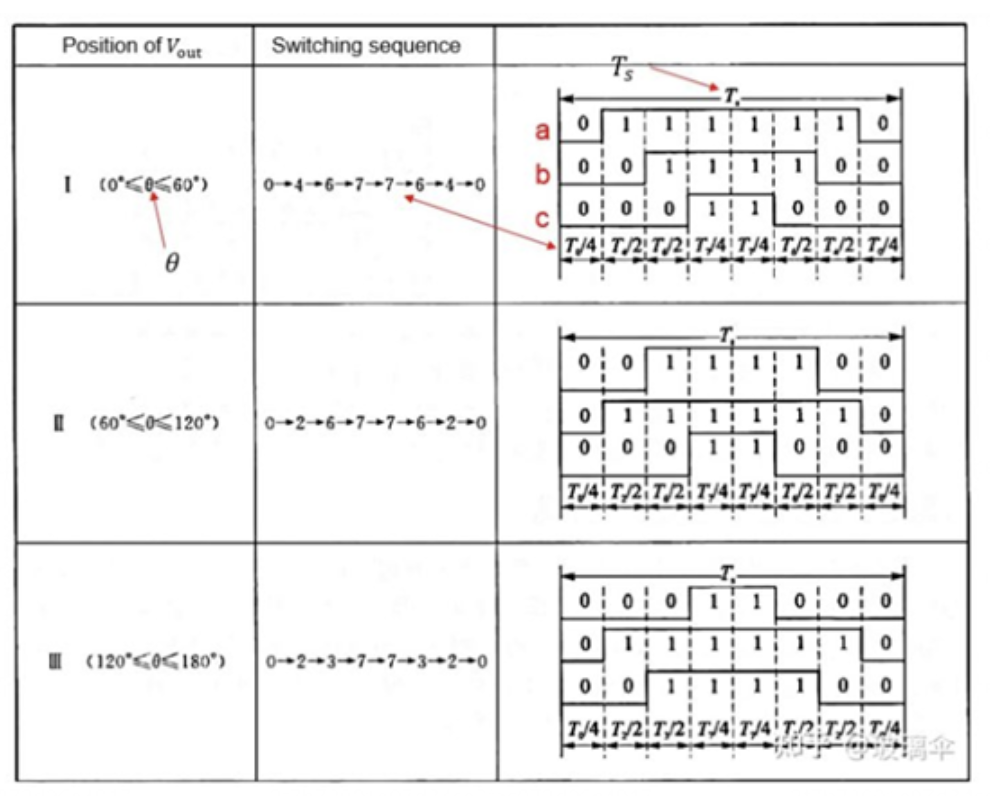
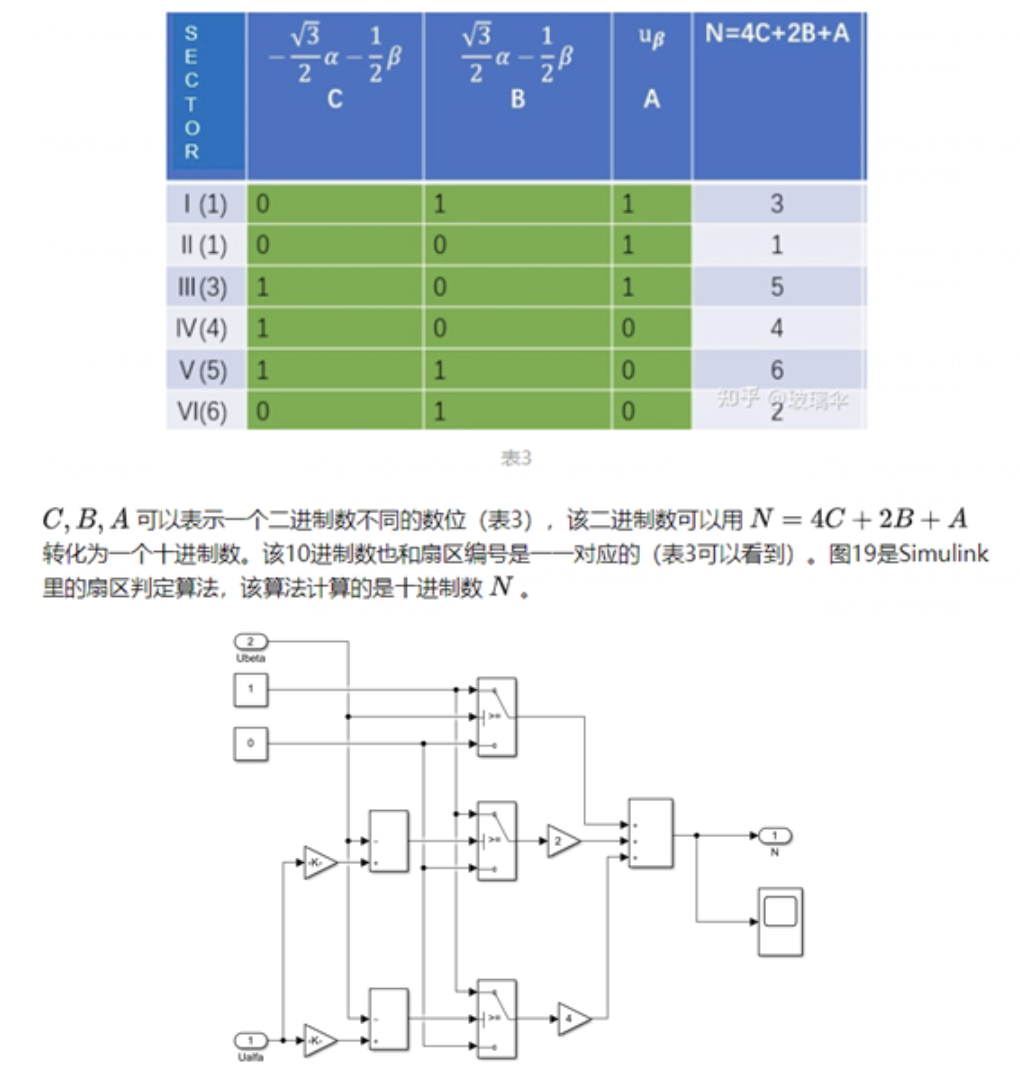
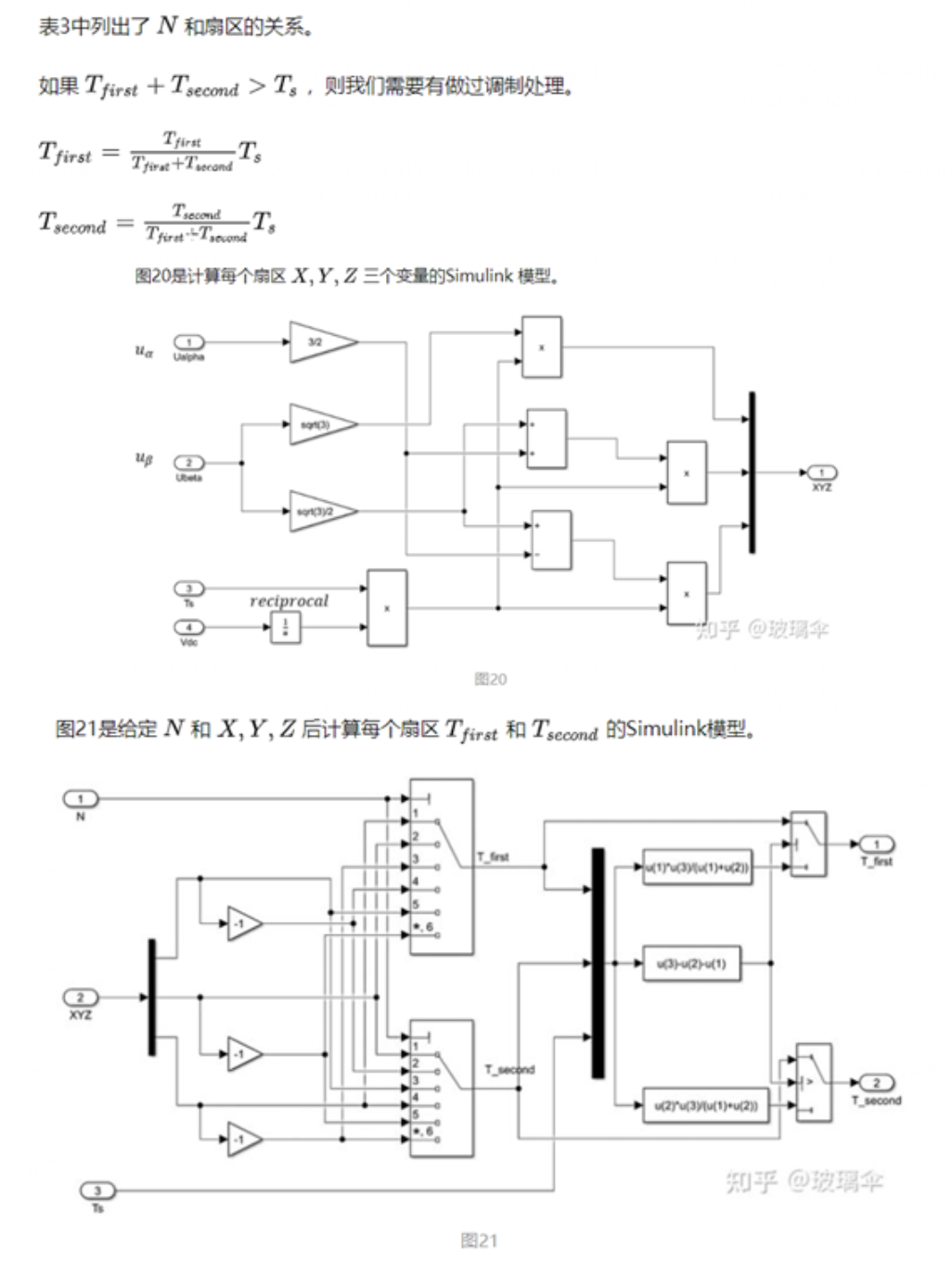
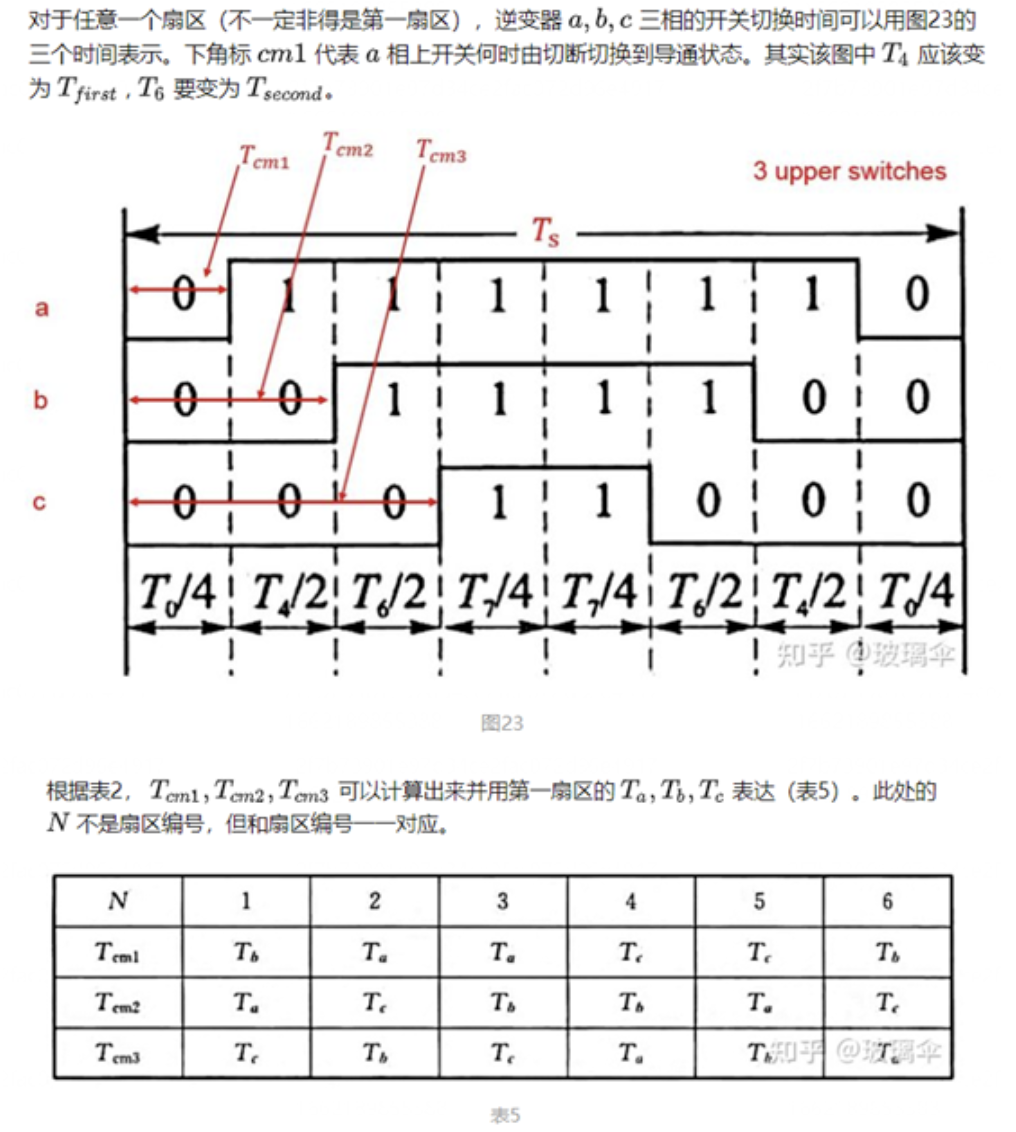
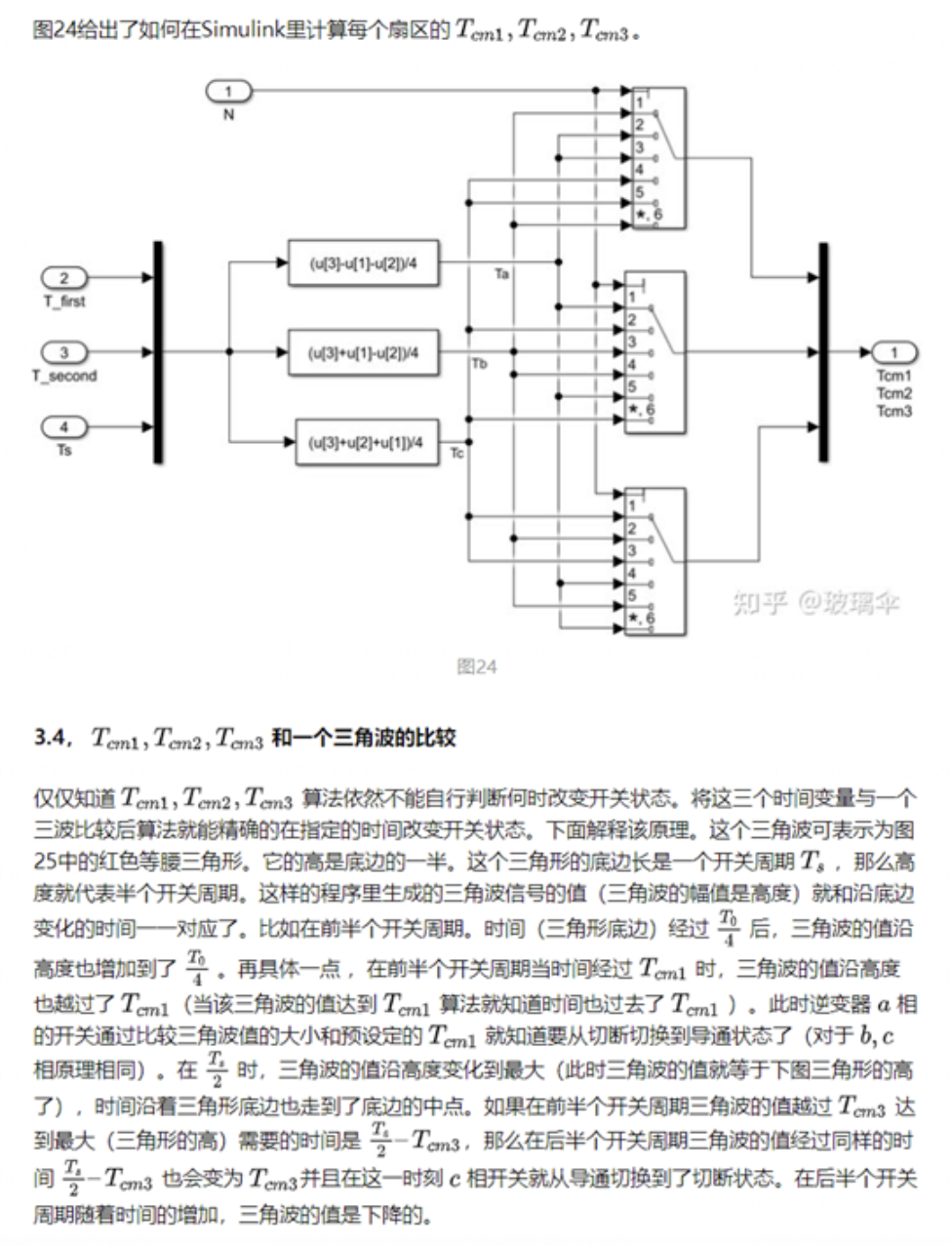
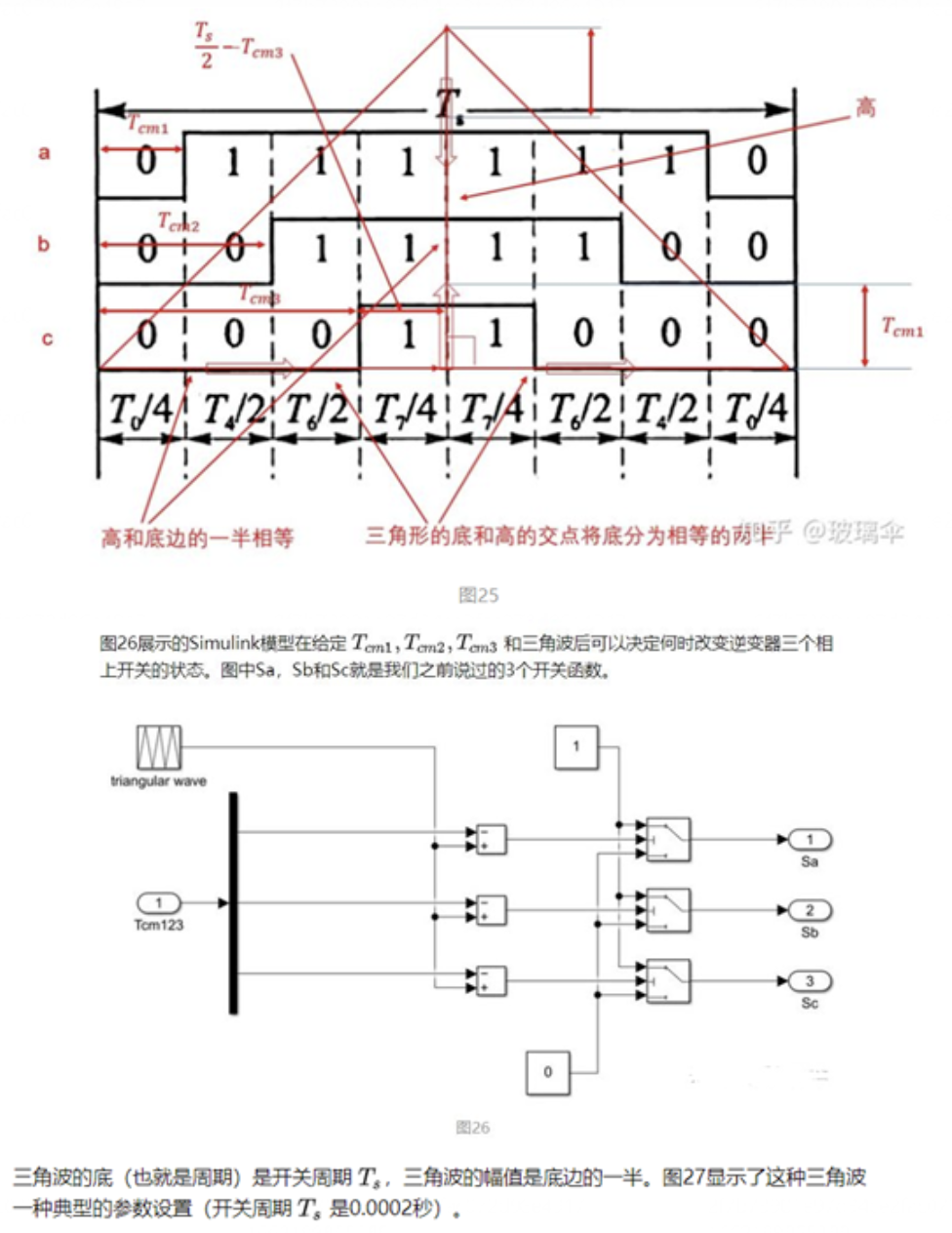
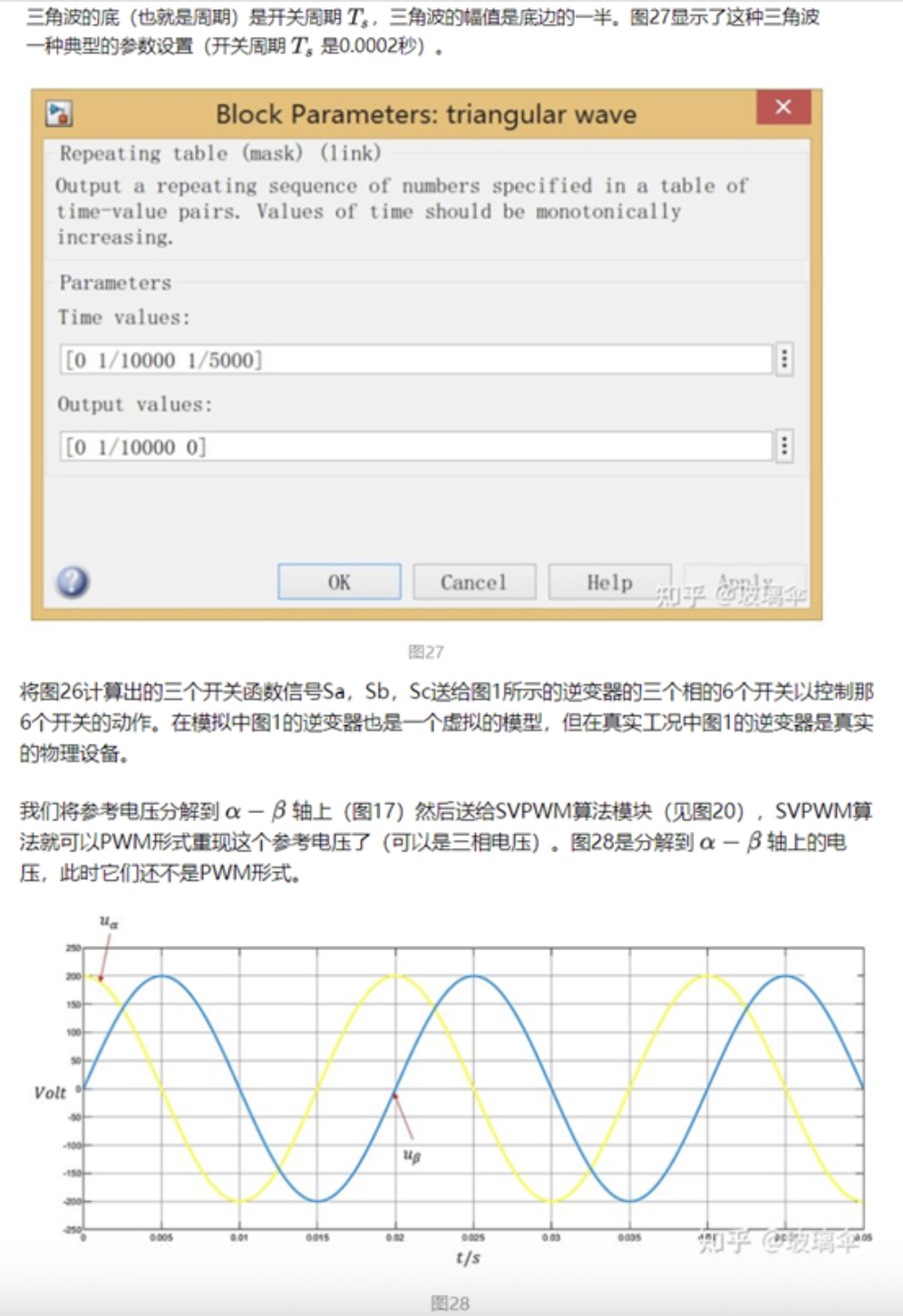
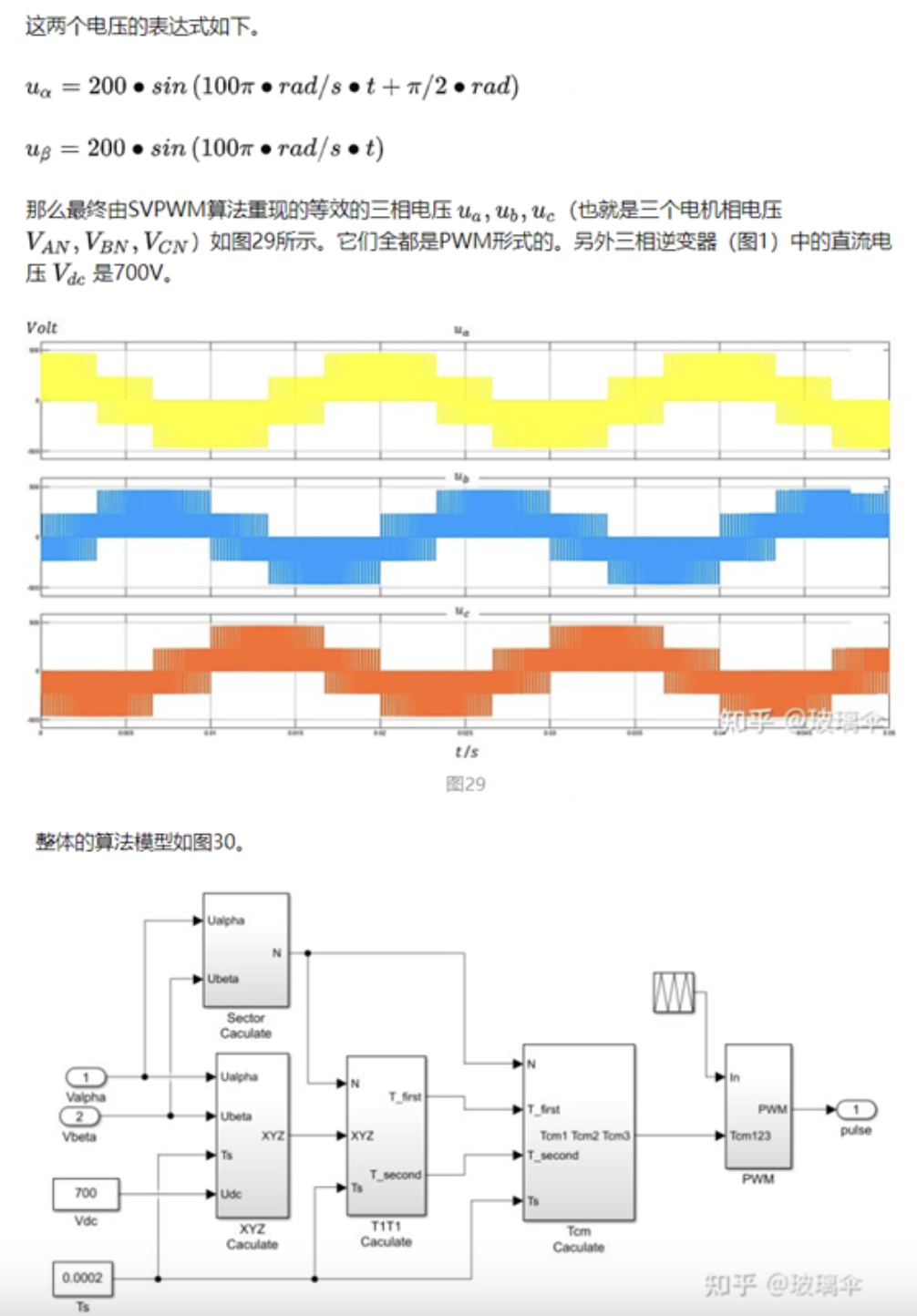
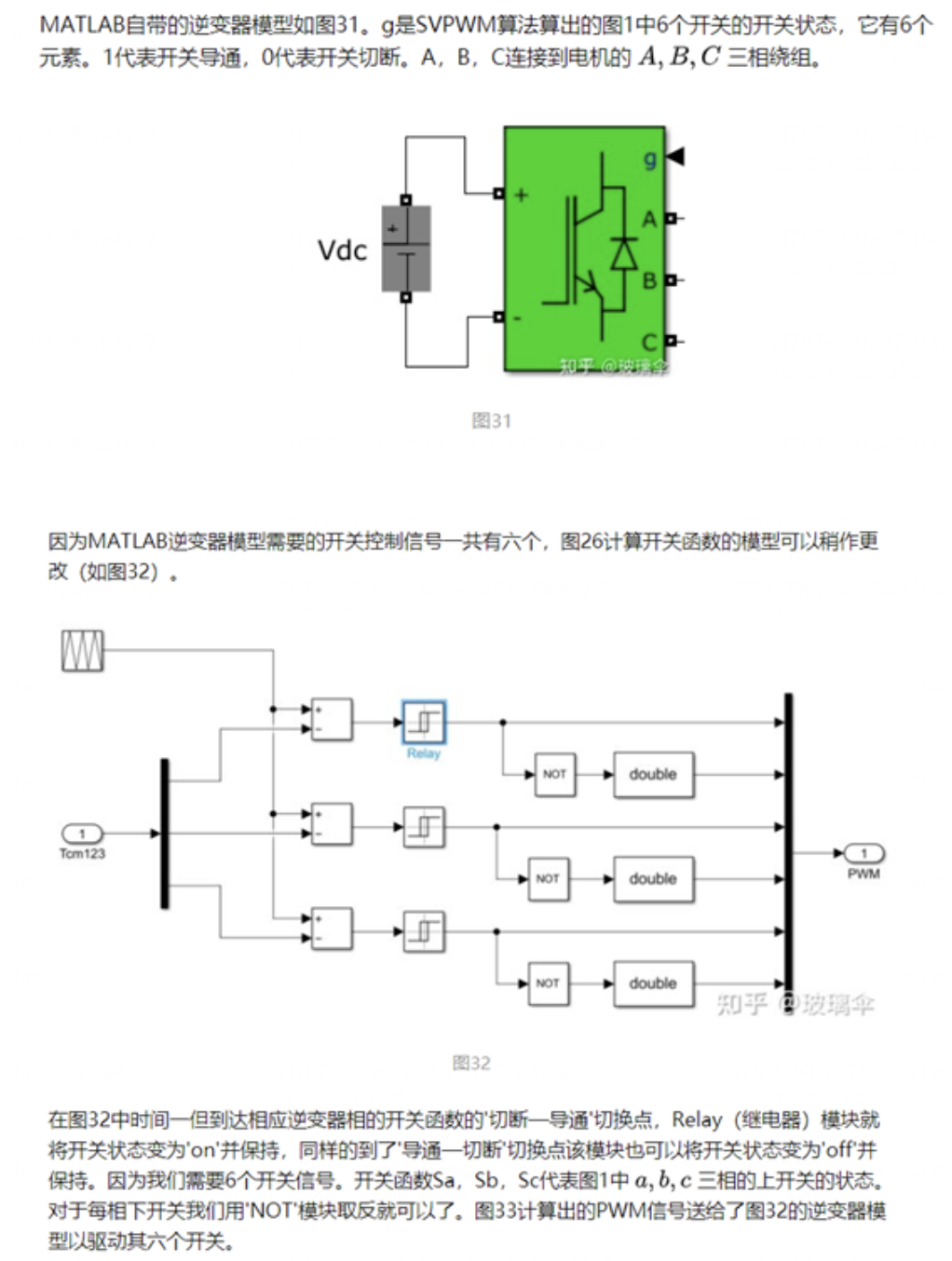
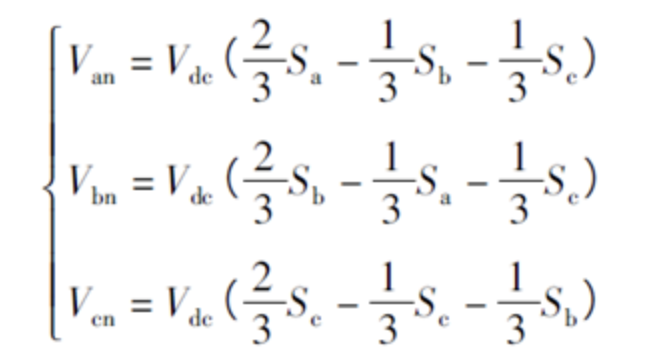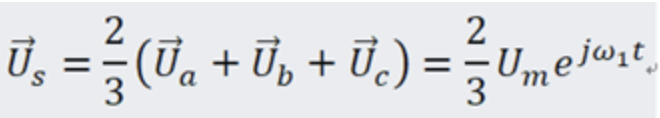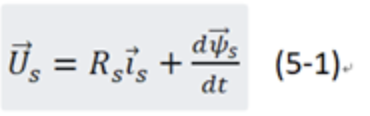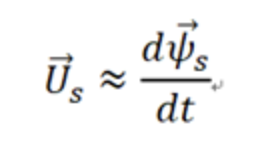导读:本期文章是对异步电机矢量控制算法的基础进行一个梳理,特别是关于SVPWM模块,给后期学习做一个参照。
一、研究背景及意义
据统计,我国有60%左右的用电量由电动机来消耗,而其中多数用于驱动异步电机。异步电机结构简单,可靠性高又易于维护,能够适应各种复杂的环境,是当前在工业现场大量使用的驱动设备。随着电力电子器件、数字处理器等技术的发展,变频控制技术已成为提高电动机运行效率和传动性能的主要技术手段。
在过去几十年,由于交流调速系统系统性能以及效率的提升,其应用领域以及应用范围越来越广泛。高性能异步电机调速控制系统不仅能满足节电需求,提高能源效率,还可以适应工业生产的工艺需求、提高我国的自动化水平。目前变频器已渗透到各行各业,其主要应用目的为节能以及工艺控制需求。对于风机水泵等性能要求一般的节能调速场合,采用简单的变压变频(VVVF)即可满足需求。但是很多工业应用场合对转速以及转矩的控制精度以及响应时间都有严格的要求,比如交通运输行业的电力牵引、冶金行业的轧钢系统、建筑行业的电梯驱动等。随着现代工业应用对调速系统的性能以及控制精度要求越来越高,这些需求使得变频控制系统难以单纯地通过提升硬件设备的性能来满足,更需要从控制的角度予以考虑解决,因此非常有必要在传统控制策略的基础上研究更为先进的控制方案。
高性能调速控制系统的设计可以视为求解一个优化问题,通常情况下,可能包含以下几个重点优化目标:
• 快速的动态响应以及尽量小的稳态跟踪误差
• 优良的运行效率以节约能源
• 较小的电流 THD 以满足相关的法规要求
• 电磁辐射以及电磁兼容问题以满足法规要求
• 共模电压抑制以提高系统的安全性以及运行寿命等
• 在整个调速范围内均能满足以上要求
目前,变频器行业在国内的市场规模逐年扩大,市场容量已超过 250 亿元。从品牌数量上来看,内资品牌占 70% 以上,但市场份额却不到 30%,尤其在高性能应用场合,内资品牌的技术积累与国外品牌还存在一定的差距,因此深入研究变频驱动技术有助于提升我国在该产业的竞争力。
二、异步电机矢量控制(FOC)
2.1有速度传感器的异步电机矢量控制(FOC)
2.1.1 FOC介绍
当前主流的高性能闭环调速系统控制方法主要有矢量控制(Field oriented control, FOC)和直接转矩控制(Direct torque control, DTC)。矢量控制通过磁场定向将定子电流分解成励磁分量和转矩分量,然后采用比例积分(proportional integral, PI)调节器在同步旋转坐标系上对其进行分别调节,最后利用空间矢量调制(Space vector modulation, SVM)等脉宽调制策略合成参考电压矢量。FOC 能取得较好的动静态性能,在中小功率场合得到了广泛的应用,但是其性能严重依赖于调节器参数的整定。由于传统的线性 PI 调节器加前馈解耦的结构存在着诸多缺陷,尤其是当系统的开关频率较低或者电机转速较高时,系统甚至不能稳定运行。为解决这一问题国内外不少学者采用包含系统控制延迟在内的精确复矢量数学模型来设计复矢量电流调节器,但是调节器参数基于连续域设计依然存在进一步改进的空间。考虑到实际数字控制系统的离散化特性,现有文献直接在离散域设计电流内环调节器,保证了系统具有良好的稳定裕度与动态特性。在矢量控制中逆变器环节仅仅被当作一个增益系统,这种上层控制算法与底层 PWM 独立分离设计的结构使得系统的整体性能存在进一步优化的空间。这是因为不同的PWM 策略对应不同的稳态性能以及逆变器开关损耗,由于系统多个控制目标之间相互耦合,单纯地从PWM 层面来优化系统的性能很难得到大幅度的改进。因此,如果在上层控制算法中就考虑逆变器不同开关状态组合对系统整体性能的影响,则能够在更大的可行解空间内获取更优的控制性能。
2.1.2 FOC工作原理
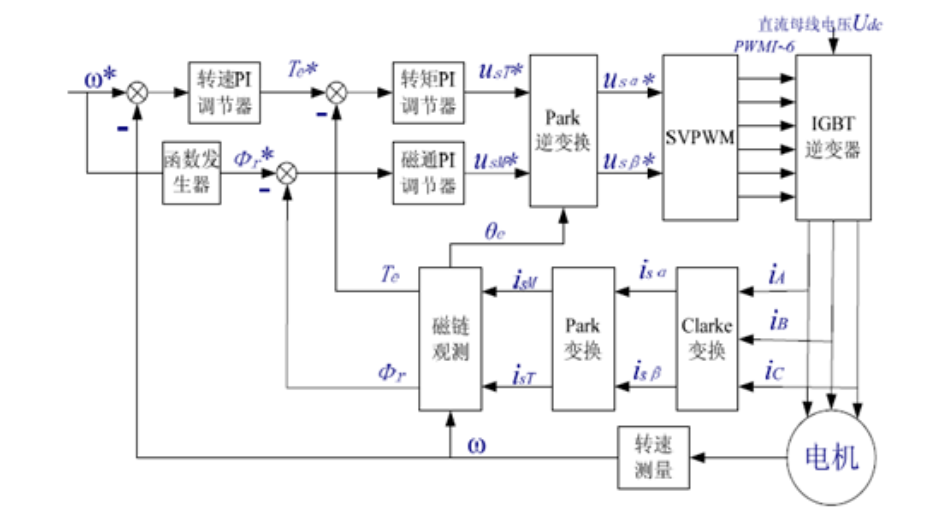
图2-1 基于SVM的异步电机矢量控制系统框图
矢量控制(Field oriented control, FOC)通过磁场定向将定子电流分解成励磁分量和转矩分量(实现对电磁转矩和转子磁链的解耦),然后采用比例积分(proportional integral, PI)调节器在同步旋转坐标系上对其进行分别调节,最后利用空间矢量调制(Space vector modulation, SVM)等脉宽调制策略合成参考电压矢量。
经过d-q 变换后的控制系统各变量均表示为旋转坐标系下的形式,此时,电机的电磁转矩可以通过控制定子电流q 轴分量来实现,而定子电流d轴分量则与感应电机的磁链幅值有关,d-q 坐标系下的电机模型对之上的关系描述如下(d-q也称为M-T)。
2.1.3 FOC系统仿真搭建及各模块介绍
异步电机矢量控制主要包括速度环、电流环、转矩环、磁链估计、坐标变换和空间电压矢量脉宽调制(SVM)模块。接下来将一一介绍各个模块的工作原理和仿真模型搭建的过程,并结合模块输出的波形进行讨论是否有更好的实现方法。特别是电压重构、转子磁链的估计方法,包括电压型磁链观测器、电流型磁链观测器、混合模型磁链观测器、全阶磁链观测器和滑模磁链观测器(可以学习一下),最后再讨论比较一下各种脉宽调制的优缺点。
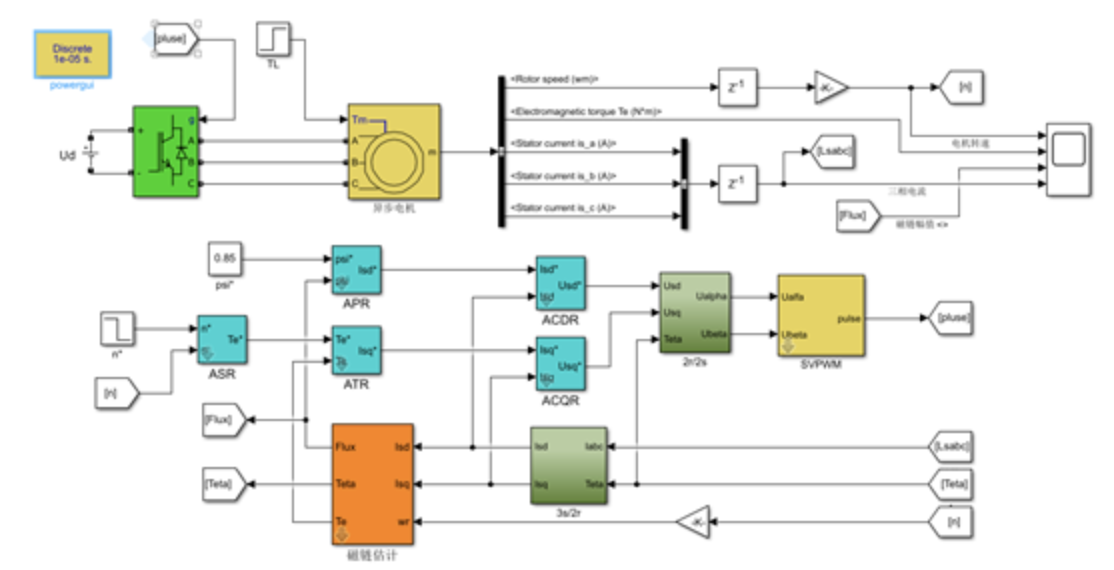
图2-2 基于SVM的异步电机矢量控制系统仿真模型
(1)电压重构(20220830)
电压重构的思路就是:直流母线电压乘以占空比得到a、b、c三相电压。重要的就是要求得占空比。
其中,Vdc为直流母线电压,Sa、Sb、Sc为SVPWM调制后的得到的三相逆变器上开关管在一个PWM周期中的导通占空比,用于重构电机定子侧电压。
a模块化获取定子电压
图2-3 三相电压获取
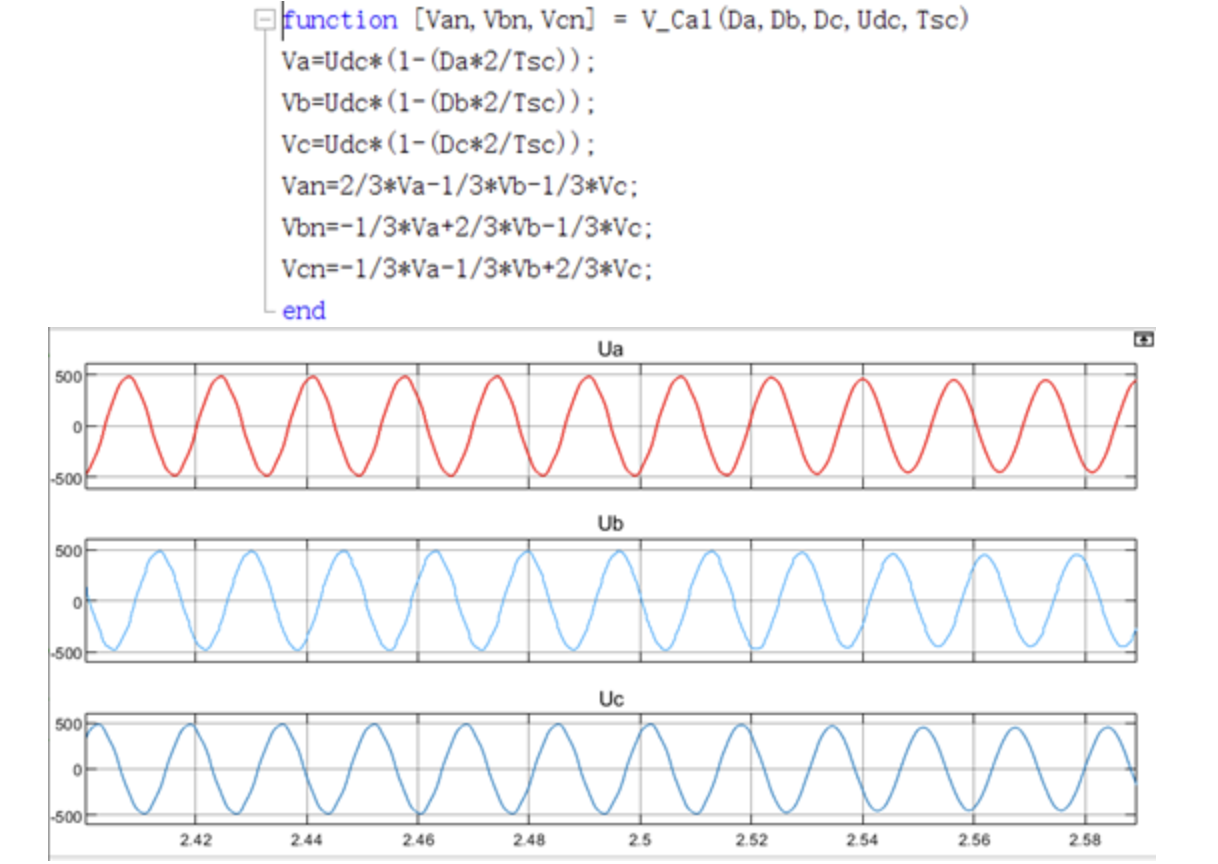
b电压重构代码实现
图2-4 三相电压重构机仿真实现
(2)坐标变换
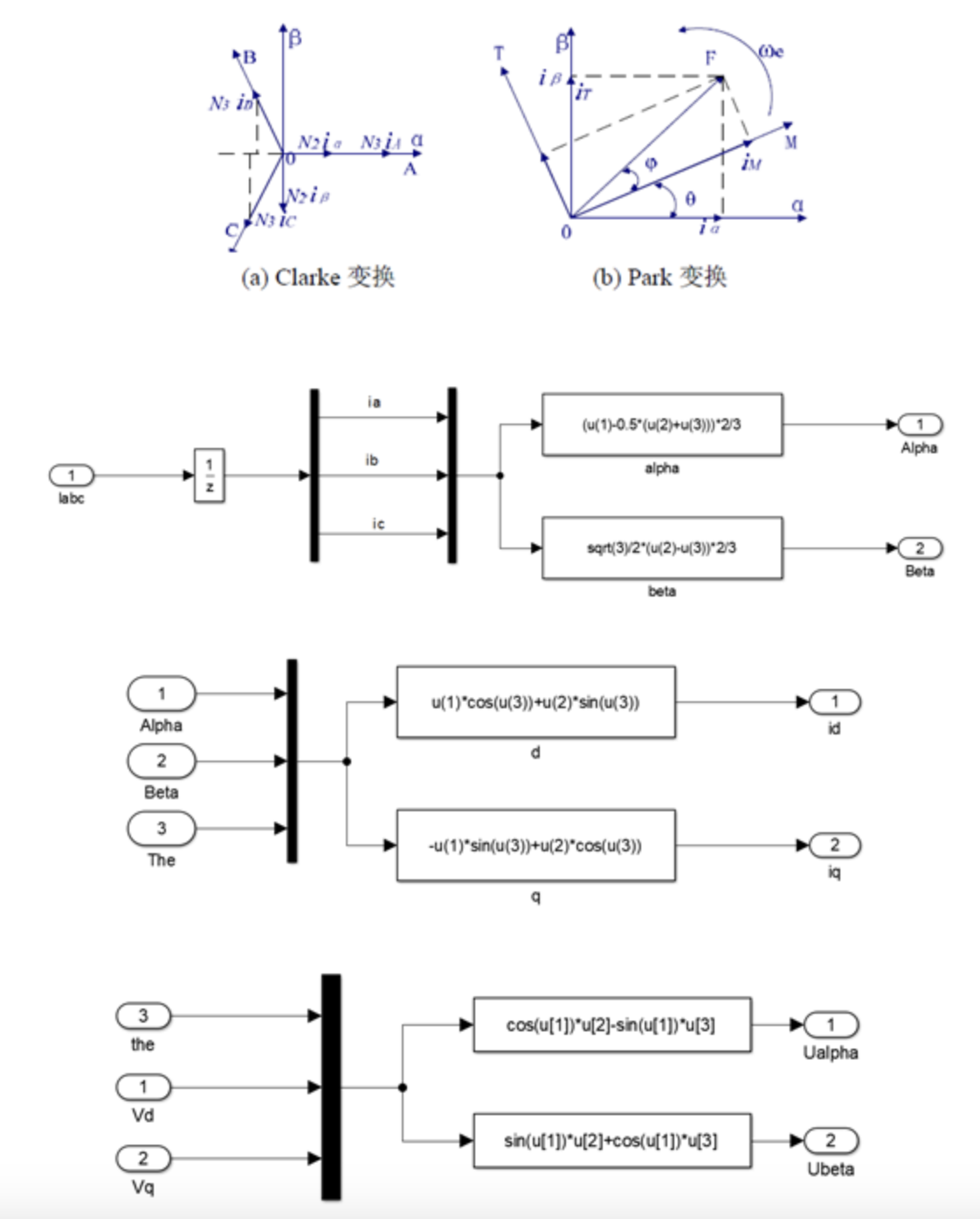
矢量控制的坐标变换有:由三相平面坐标系向两相静止平面直角坐标系的转换,称之为Clarke 变换(也叫3s/2s 变换);由两相静止平面直角坐标系向两相旋转直角坐标系的转换,称之为Park 变换(也叫2s/2r 变换);以及它们的逆变换。
在矢量坐标变换中需要遵循的两个原则是:一是变换前后的电流所产生的旋转磁场等效;二是变换前后两个系统的电机功率保持不变。
图2-5 坐标变换
(3)磁链估计
后期文章会单独介绍;
(4)PI电流调节器介绍
后期文章会单独介绍;在此写一些关于PI电流调节器的思考总结。
总结:
PI电流调节器是矢量控制中的重要模块之一。矢量控制的控制性能依赖内环PI电流调节器的参数整定,所以对PI电流调节器的设计至关重要。
思考:
为什么电压量自经过PID控制器就变成电流量?电流量自经过PID控制器就变为电压量?
(5)空间电压矢量脉宽调制技术(SVM)(重点)
电压空间矢量调制技术(SVPWM ,Space Vector Pulse Width Modulation)是从控制电机中推导出来的。SVPWM是依据交流器空间电压矢量切换来控制交流器的一种控制策略,其主要思想在于抛弃原有的SPWM算法,采用逆变器空间电压矢量的切换以获得准圆形旋转磁场,从而在不高的开关频率条件下,使得交流电机获得较SPWM算法更好的控制性能。
SVPWM算法实际上是对应于交流电机中三相电压源逆变器功率器件的一种特殊的开关触发顺序的脉宽大小的组合,这种开关触发顺序和组合将在定子线圈中产生三相互差120°的电角度、失真较小的正弦波电流波形。实践和理论证明,与直接的SPWM技术相比,SVPWM算法的优点主要有:
(1)SVPWM优化谐波程度比较高,消除谐波效果要比SPWM好,实现容易,并且可以提高电压利用率;
(2)SVPWM算法提高了电压源逆变器的直流电压利用率和电机的动态响应速度,同时减小了电机的转矩脉动等缺点;
空间矢量控制 (SVPWM) 技术与传统意义上的正弦脉宽调制 (SPWM) 相比,空间矢量控制技术的电流谐波成份更加的少,从而使电机转矩的脉动大大减小,有利于电机使用寿命的提高。并且空间矢量控制技术对直流侧母线的利用率比 SPWM技术提高了15.4%。空间矢量技术采用的是互补导通方式,并且每一次都只有一个开关动作,所以一周期内,开关的使用频率大幅减少,从而能够延长功率开关器件的使用时间,减少功率开关器件的损耗。空间矢量控制技术的优越性,使其成为未来电机控制的主流技术.
注:SVPWM电压利用率提高15.4%分析!
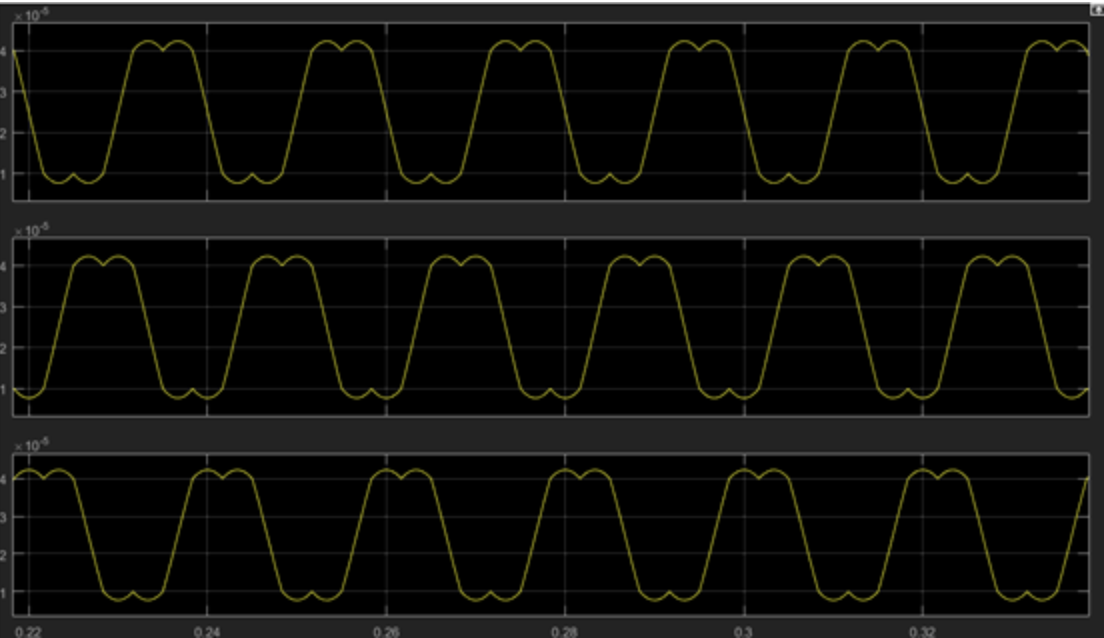
从分析理解马鞍波的角度去解释SVPWM相比较于SPWM,电压利用率提高了15.4%:SVPWM产生了马鞍波,马鞍波也会产生正弦波的电流。从图中可以发现,马鞍波就是被拉宽的正弦波,拉宽了就代表相电压的持续时间边长了,所以就提高了母线电压的利用率,电机的动态响更好。
当调制比为1时,SPWM相电压的峰值是母线电压的0.5倍,而SVPWM的相电压峰值是母线电压的0.557倍,也就是根号3/3。SVPWM(0.557)/SPWM(0.5)=1.1547,所以SVPWM的电压利用率相比较于SPWM,提高了15.47%。
马鞍波(SVPWM)
(3)SVPWM比较适合于数字化控制系统。
5.1)空间电压矢量的定义
这意味着三相对称正弦电压所合成的空间矢量是一个在空间中等幅恒速旋转的矢量。并且合成的空间电压矢量的幅值是原来的正弦量幅值的1.5倍。通常,希望空间电压矢量与原来三相对称正弦量的幅值相同,于是,空间矢量可以定义为:
5.2)三相异步电机定子端电压与定子磁链矢量之间的关系
当电机转速不是很低时,定子电阻上的压降对于定子磁链产生的感应电动势来说较小,可以忽略。
在电机学中,当电机由三相平衡正弦电压供电时,电动机定子磁链幅值恒定,其空间矢量以恒速、等幅值旋转,它的矢量端的运动轨迹呈圆形,一般称为矢量圆。定子磁链旋转矢量可用下式表示:
当磁链幅值一定时,电压空间矢量的大小与供电电压频率成正比,其方向与磁链矢量正交,即磁链圆的切向方向。当磁链矢量在空间旋转一周时,电压矢量也连续地按磁链圆的切线方向运动2弧度,其轨迹也是圆形的。这样,电动机旋转磁场的轨迹问题就可转化为电压空间矢量的运动轨迹问题。
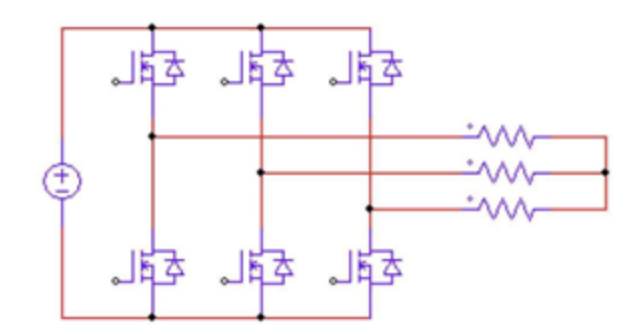
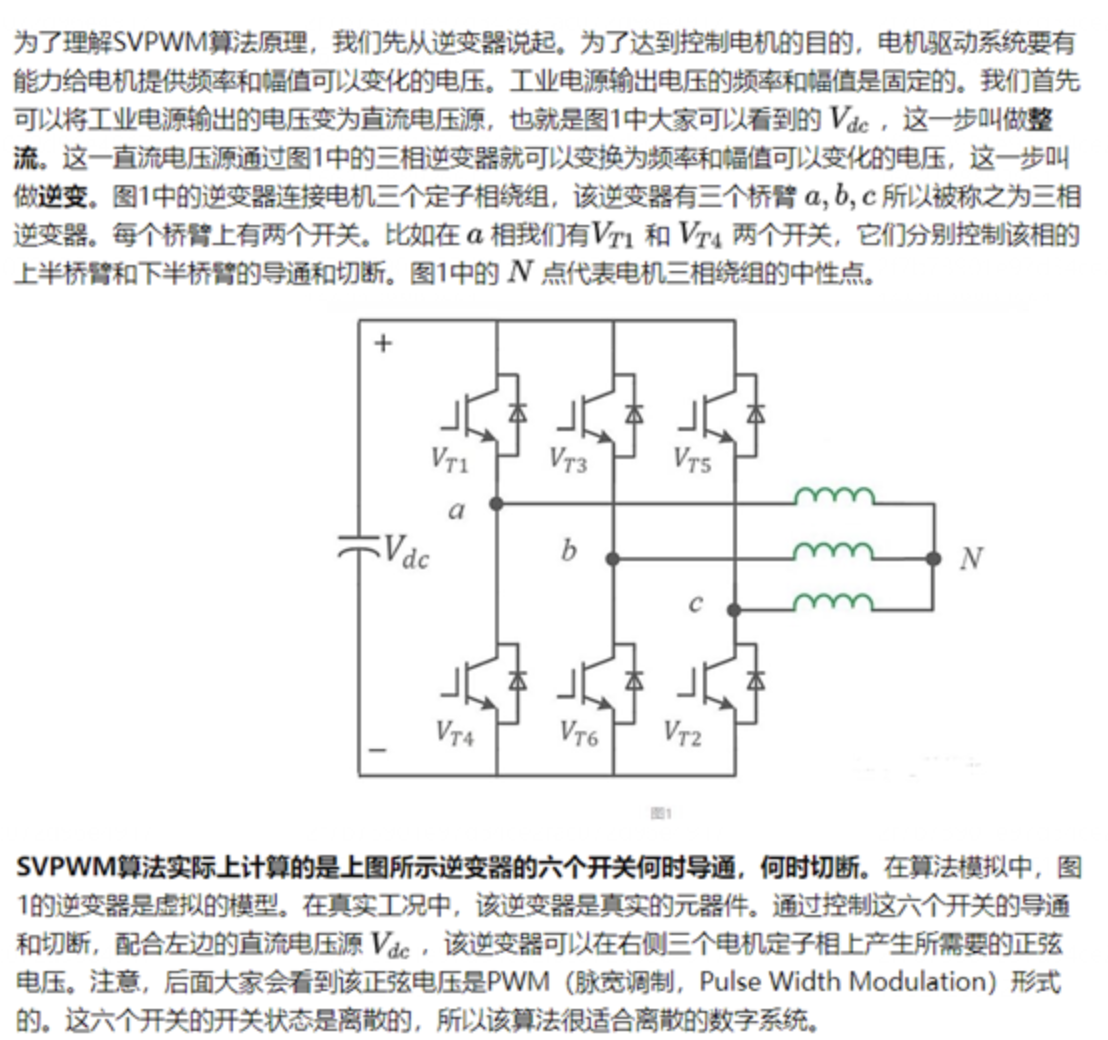
5.3)三相全桥电压型PWM逆变器的八个电压空间矢量
图4-9 三相桥式逆变电路
电压源型PWM逆变器同一桥臂的上、下开关管驱动信号互补。三个桥臂各自独立,每个桥臂有两种开关状态,2 2 2=8,三相全桥电压型PWM逆变器总共可以输出8个电压空间矢量。
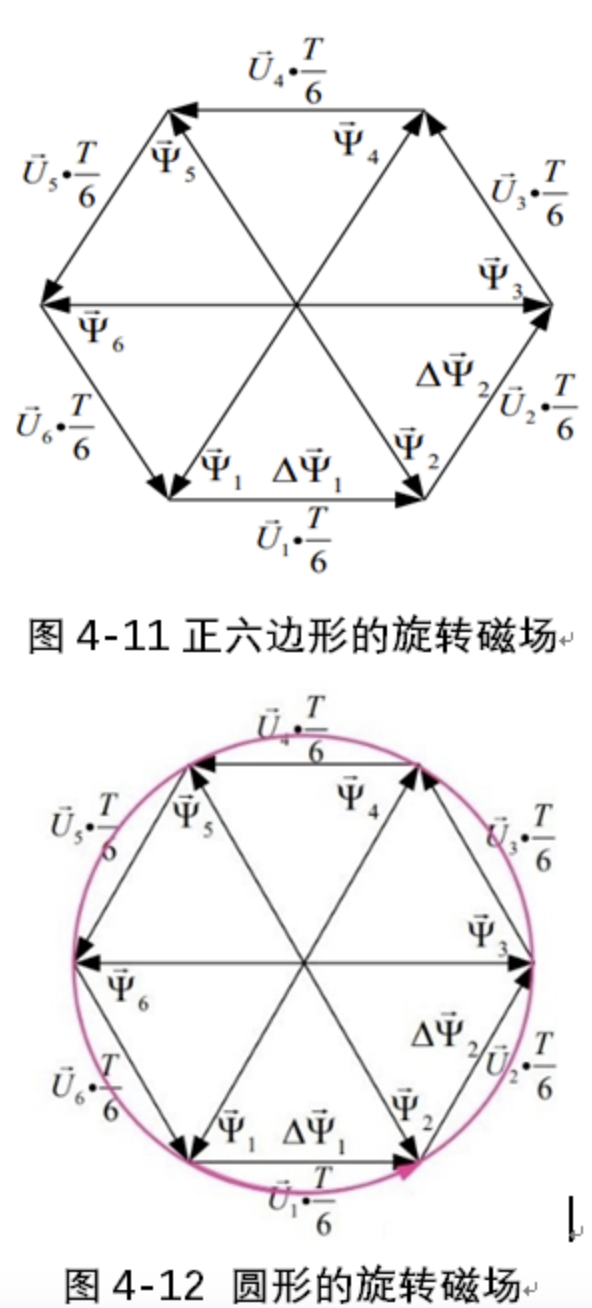
5.4)正六边形空间旋转磁场
6个有效空间电压矢量,在一个输出基波电压周期内各自依次连续作用1/6周期,逆变器运行于这种状态时会得到一个正六边形的旋转磁场。六个有效电压矢量各自连续作用1/6T,显然不能得到一个圆形的旋转磁场。所以这种六拍阶梯波逆变器的性能较差。
电机转动形成圆形的旋转磁场。如何使逆变器输出的正六边形的旋转磁场变成一个圆形旋转磁场?
(1)、图4-11中磁链矢量为何与电压矢量不垂直?
输入电压不是正弦,得到的磁链不是圆形旋转的,其幅值也在变化,所以相位就不再是相差。
(2)、SVPWM作用和目标?
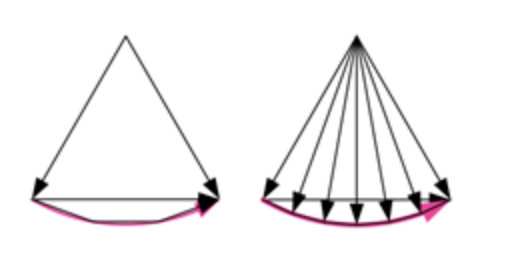
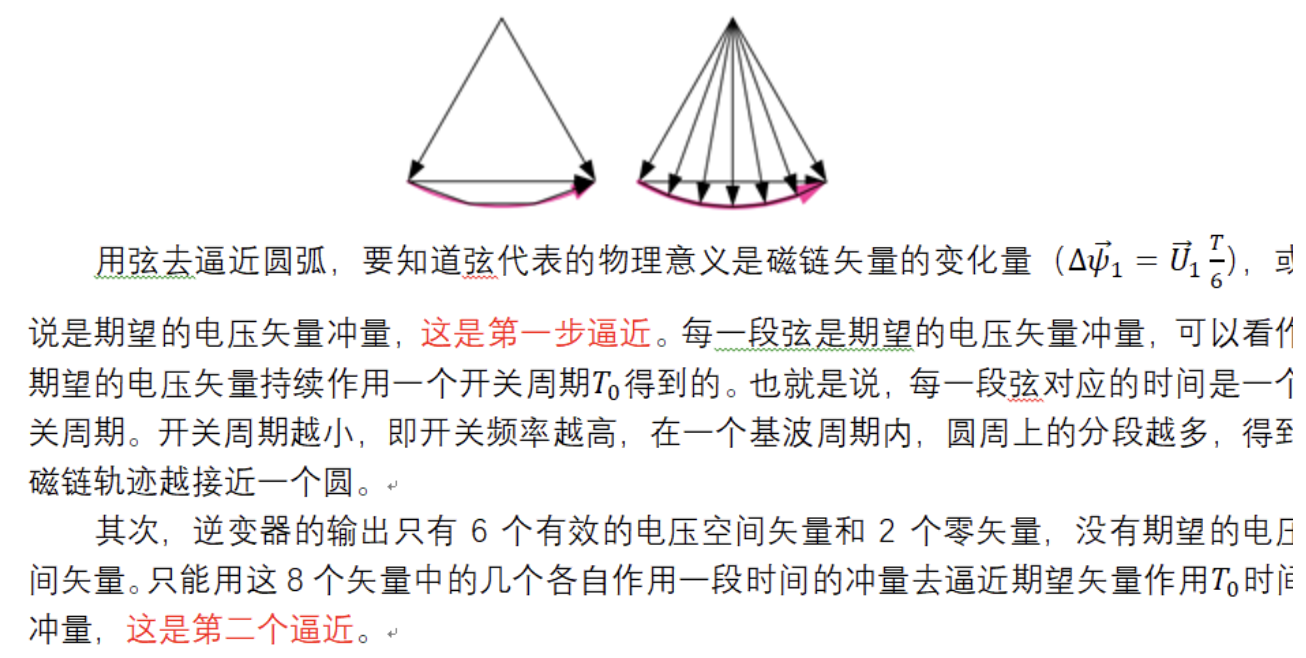
在每个1/6T之内,磁链的变化为一段圆弧,而不是一段弦。真正的圆弧肯定是得不到的,除非用理想的正弦电压供电。但这是目标,可不可以设法尽可能地逼近这个目标?
可以用一段一段的弦来逼近圆弧。分段越多,越接近圆弧。如何得到一段一段的弦?
5.5)空间电压矢量调制(SVPWM)
如图4-11可知,8个电压矢量形成一个六边形,这和电机原理的圆形磁场还相差很远,所以电压输出效果肯定不好。众所周知,矢量之间可以进行合成,那么我们就用8个电压矢量进行合成,得到想要的电压矢量从而可以得到接近圆形的电压矢量。这就是电压空间矢量(SVPWM)的基本思想。
5.6)SVPWM实现过程
从上节的分析可知,哪几个电压空间矢量和其作用的时间是SVPWM的两个根本的问题。要实现SVPWM,仿真搭建时需要注意和解决的几个问题。
(1)、电压空间矢量所在扇区的判断;
(2)、基本矢量作用时间的计算;
(3)、基本矢量的作用顺序及扇区切换点时间确定。
只要解决以上3个问题,就能实现SVPWM。
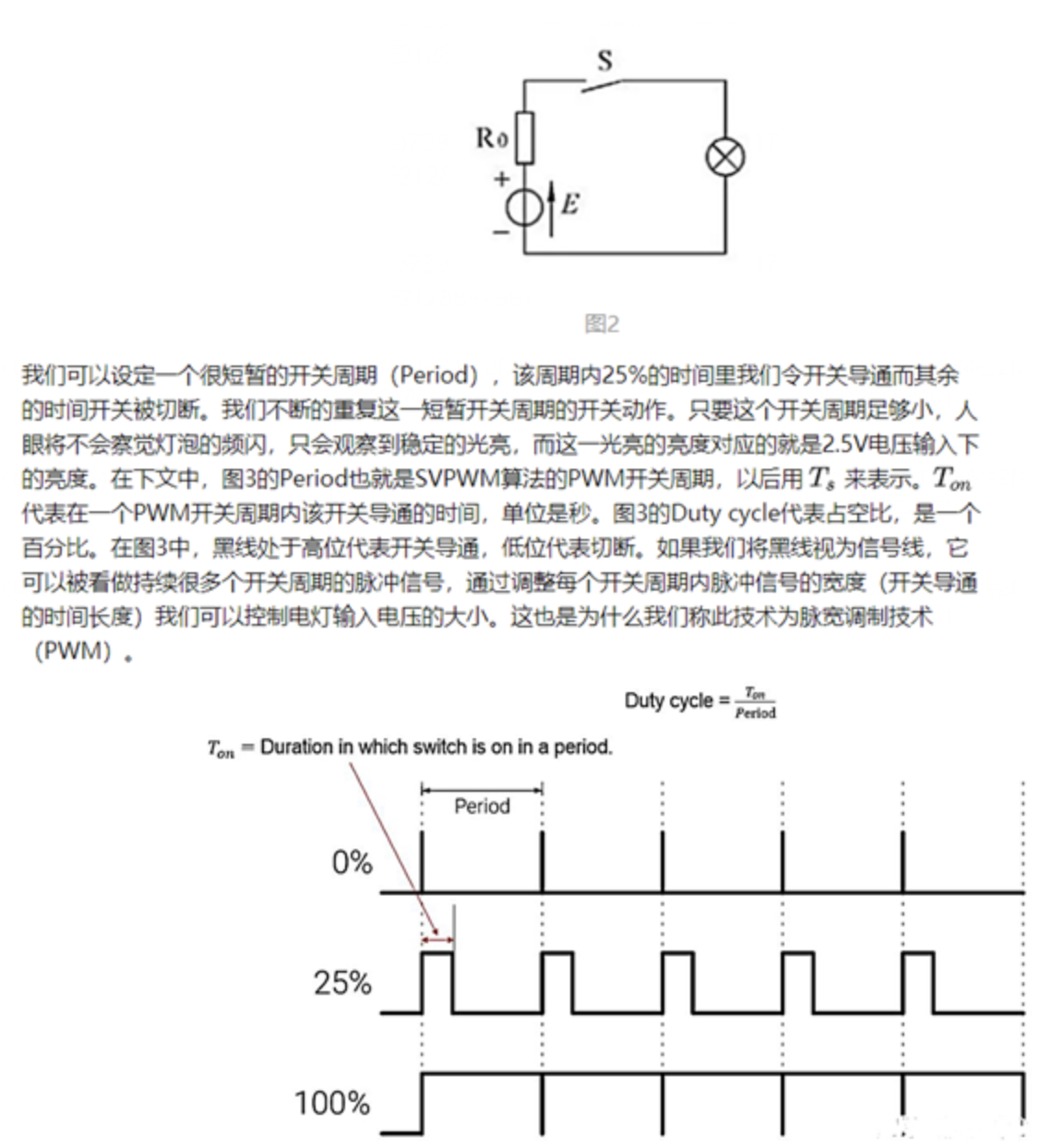
下面我们用一个小例子来理解PWM信号。图2是一个直流电路,它有一个电阻,一个开关,一个灯泡,和一个驱动灯泡的10V直流电压源。我们如何能得到2.5V电压驱动下的灯泡亮度呢?
5.6.1)SVPWM理论讲解
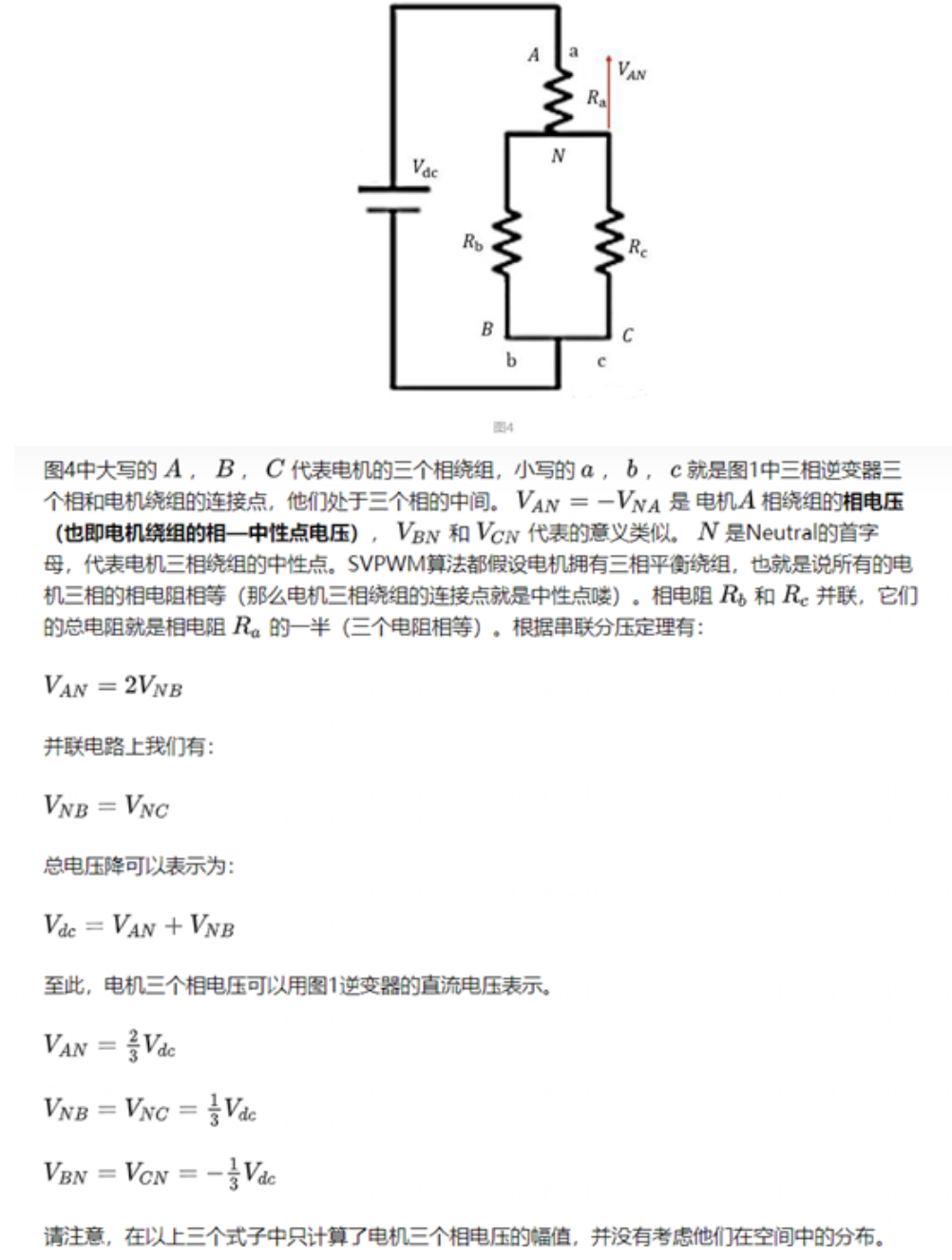
该状态对应的电机绕组连接图如下:
5.6.1)扇区判断
5.6.2)基本矢量作用时间计算
5.6.3)基本矢量的作用顺序及扇区切换点时间确定
5.7)小结
电压空间矢量调制技术(SVPWM ,Space Vector Pulse Width Modulation)是从控制电机中推导出来的。由于电机旋转时产生圆形的旋转磁场,可以把逆变器和交流电机当成是一个整体考虑,按照交流电机产生圆形磁场来控制逆变器,这时的逆变器输出波形会更好。SVPWM也可以叫磁链跟踪控制,它是在假象的静止坐标系下控制不同电压矢量得到的。SVPWM算法的理论基础是平均值等效原理,即在一个开关周期Ts内通过对基本电压矢量加以组合,使其平均值与给定电压矢量相等。所以SVPWM的实质就是用逆变器可输出的电压空间矢量与作用时间的线性组合去逼近所期望的电压空间矢量,具体的做法就是对逆变器中功率器件的开通和关断状态进行正确控制。
2.2仿真建模
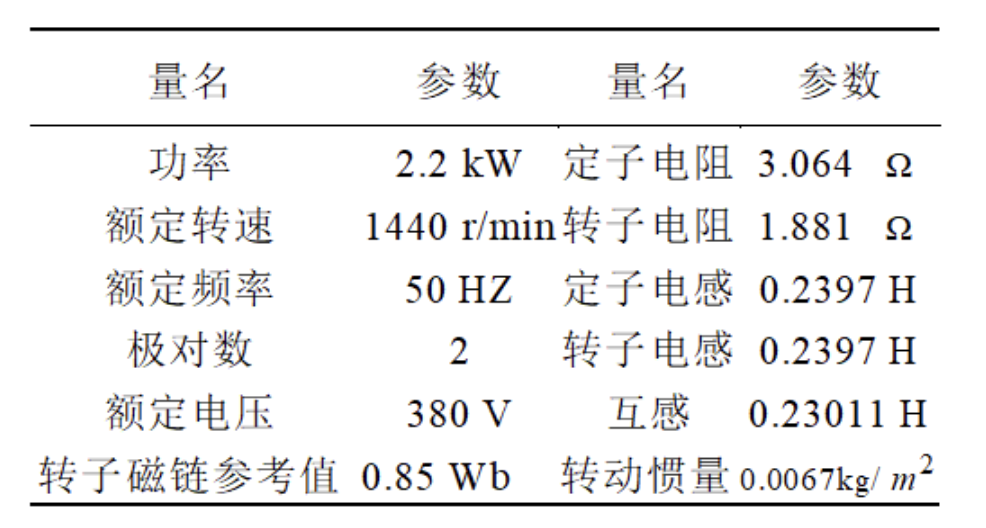
2.2.1电机参数
2.2.2电机运行的工况
仿真中异步电机的参数如上表所示。仿真运行的采样率为5K,在0.7秒前,速度参考值设为1500r/min,在0.7秒后参考速度设置为1000r/min。在0.4秒前,电机空载,在0.4秒之后给电机加14N.m的负载。
2.2.3仿真波形分析
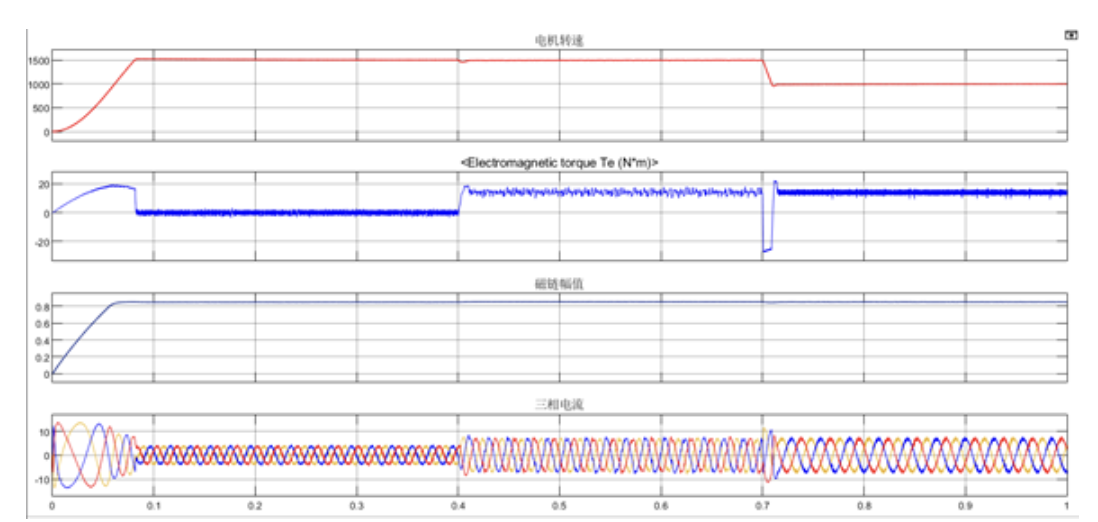
图2-6 仿真波形变化情况
从上图可知,电机转速动态响应快,实际值能快速跟踪上参考值。在突加载的情况下,速度有跌落的现象,但能够快速恢复到原稳态值。转矩分量和励磁分量能够实现完全解耦,且定子电流随电机的加载情况做出相应的变化。整体来说,仿真运行的情况与理论相符,验证所搭的异步电机矢量控制仿真系统的可行性和有效性。
2.3、总结
FOC控制的本质其实就是解耦。借助电角度,把三相侧电流变换到旋转两相侧(也就是clark,park变换),然后在旋转两相侧实现转矩和磁链的单独控制。以上的分析都是依托于MATLAB/simulink仿真进行的,接下来会尝试进行硬件平台方面的设计和实现并结合现在工业中使用的FOC进一步深化学习异步电机矢量控制。
作者:浅谈电机控制
来源:浅谈电机控制
推荐阅读
更多电机控制技术干货请关注电机控制专栏。
迎添加极术小姐姐微信(id:aijishu20)加入技术交流群,请备注研究方向。