在现代数据分析领域,时间序列数据的处理和预测一直是一个具有挑战性的问题。随着物联网设备、金融交易系统和工业传感器的普及,我们面临着越来越多的高维时间序列数据。这些数据不仅维度高,而且往往包含复杂的时间依赖关系和潜在模式。传统的时间序列分析方法如移动平均等,在处理此类数据时往往显得力不从心。
基于矩阵分解的长期事件(Matrix Factorization for Long-term Events, MFLEs)分析技术应运而生。这种方法结合了矩阵分解的降维能力和时间序列分析的特性,为处理大规模时间序列数据提供了一个有效的解决方案。
核心概念
矩阵分解
矩阵分解(Matrix Factorization)是将一个矩阵分解为多个基础矩阵的乘积的过程。在时间序列分析中,最常用的是奇异值分解(Singular Value Decomposition, SVD)。SVD 可以将原始矩阵 A 分解为:
A = USV^T
其中:
- U 和 V 是正交矩阵
- S 是对角矩阵,对角线上的元素称为奇异值
潜在变量与潜在特征
- 潜在变量(Latent Variables):指数据中无法直接观测但实际存在的变量,它们往往是多个可观测变量的综合表现。
- 潜在特征(Latent Features):通过矩阵分解得到的低维表示,它们是潜在变量在数学上的具体体现。每个潜在特征可能代表多个原始特征的组合。
维度降低在时间序列分析中的意义
维度降低(Dimensionality Reduction)在时间序列分析中具有多重意义:
计算效率:
- 原始维度下的计算复杂度:O(n^3),其中 n 为特征数量
- 降维后的计算复杂度:O(k^3),其中 k 为降低后的维度数,通常 k << n
噪声过滤:
- 较小的奇异值通常对应噪声分量
- 保留主要奇异值可以实现数据去噪
模式提取:
- 帮助发现时间序列中的主要趋势和季节性模式
- 便于识别多个时间序列之间的相关性
主成分分析(PCA)与 MFLE 的关系
主成分分析(Principal Component Analysis, PCA)是一种经典的降维方法,而 MFLE 可以看作是 PCA 在时间序列领域的扩展应用。与 PCA 相比,MFLE 具有以下特点:
- 时间敏感性:考虑数据点之间的时间依赖关系
- 预测能力:能够基于历史模式进行预测
- 多序列建模:可以同时处理多个相关的时间序列
MFLE 的数学基础
MFLE 的核心思想是将时间序列数据矩阵 X ∈ ℝ^(m×n) 分解为两个低维矩阵的乘积:
X ≈ WH
其中:
- W ∈ ℝ^(m×k) 表示基矩阵(basis matrix)
- H ∈ ℝ^(k×n) 表示编码矩阵(encoding matrix)
- k 是潜在特征的数量,通常 k << min(m,n)
这种分解通过最小化以下目标函数来实现:
min ||X - WH||F^2 + λ(||W||F^2 + ||H||\_F^2)
其中:
- ||·||\_F 表示 Frobenius 范数
- λ 是正则化参数,用于防止过拟合
长期事件(MFLEs)技术实现
数据准备与预处理
importnumpyasnp
importpandasaspd
fromsklearn.decompositionimportTruncatedSVD
fromsklearn.linear_modelimportLinearRegression
fromsklearn.model_selectionimporttrain_test_split
importmatplotlib.pyplotasplt
## 生成合成数据
np.random.seed(42)
n_series=100 ## 时间序列的数量
n_timepoints=50 ## 时间点的数量
## 模拟数据矩阵(行:时间序列,列:时间点)
data_matrix=np.random.rand(n_series, n_timepoints)
df=pd.DataFrame(data_matrix)
print(df.head())在这个实现中,我们选择了 100 个时间序列,每个序列包含 50 个时间点。这些参数的选择基于以下考虑:
- n_series = 100:提供足够的样本量以捕获不同的模式
- n_timepoints = 50:足够长以体现时间序列的特性,又不会造成过大的计算负担
矩阵分解实现
svd=TruncatedSVD(n_components=10) ## 降至10个潜在特征
latent_features=svd.fit_transform(data_matrix)
## 重构时间序列
reconstructed_matrix=svd.inverse_transform(latent_features)关键参数说明:
n_components = 10
- 选择理由:通常选择能解释 80-90%方差的特征数量
- 计算成本:与特征数量的三次方成正比
- 最佳实践:可以通过 explainedvariance_ratio确定
截断 SVD(TruncatedSVD)
- 优势:内存效率高,计算速度快
- 适用场景:大规模稀疏矩阵
- 数学原理:只计算前 k 个最大奇异值
预测模型构建
## 准备训练和测试数据集
X=latent_features[:, :-1]
y=latent_features[:, -1]
X_train, X_test, y_train, y_test=train_test_split(X, y, test_size=0.2, random_state=42)
## 训练回归模型
model=LinearRegression()
model.fit(X_train, y_train)
## 进行预测
y_pred=model.predict(X_test)模型选择考虑:
线性回归
- 优势:计算效率高,可解释性强
- 局限:仅能捕获线性关系
- 适用场景:潜在特征间的关系较为简单时
数据分割(test_size=0.2)
- 标准做法:留出 20%作为测试集
- 注意事项:需要考虑时间序列的连续性
可视化分析
单序列重构效果分析
"""
原始与重构时间序列的对比
"""
importmatplotlib.pyplotasplt
## 绘制原始与重构时间序列的对比图
series_idx=0 ## 选择特定的时间序列
plt.figure(figsize=(10, 6))
plt.plot(data_matrix[series_idx, :], label="Original", marker="o")
plt.plot(reconstructed_matrix[series_idx, :], label="Reconstructed", linestyle="--")
plt.title("MFLE: Original vs Reconstructed Time Series")
plt.xlabel("Time")
plt.ylabel("Values")
plt.legend()
plt.grid()
plt.show()可视化结果解读:
重构质量评估
- 曲线吻合度反映了模型捕获主要模式的能力
- 偏差主要出现在局部波动处
- 整体趋势被很好地保留
噪声过滤效果
- 重构序列更平滑
- 去除了高频波动
- 保留了主要趋势
综合性能评估
importmatplotlib.pyplotasplt
importseabornassns
## 设置绘图
fig, axes=plt.subplots(2, 2, figsize=(15, 12))
fig.suptitle('Time Series Analysis and Prediction', fontsize=16)
## 1. 原始数据与重构数据对比(第一个时间序列)
axes[0, 0].plot(data_matrix[:1].T, 'b-', alpha=0.5, label='Original')
axes[0, 0].plot(reconstructed_matrix[:1].T, color="Red", label='Reconstructed')
axes[0, 0].set_title('Original vs. Reconstructed Data')
axes[0, 0].set_xlabel('Time Points')
axes[0, 0].set_ylabel('Value')
axes[0, 0].legend()
## 2. 解释方差比
explained_variance_ratio=svd.explained_variance_ratio_
cumulative_variance_ratio=np.cumsum(explained_variance_ratio)
axes[0, 1].plot(range(1, len(explained_variance_ratio) +1), cumulative_variance_ratio, 'bo-')
axes[0, 1].set_title('Cumulative Explained Variance Ratio')
axes[0, 1].set_xlabel('Number of Components')
axes[0, 1].set_ylabel('Cumulative Explained Variance Ratio')
axes[0, 1].set_ylim([0, 1])
## 3. 实际值与预测值对比
axes[1, 0].scatter(y_test, y_pred)
axes[1, 0].plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=2)
axes[1, 0].set_title('Actual vs. Predicted Values')
axes[1, 0].set_xlabel('Actual Values')
axes[1, 0].set_ylabel('Predicted Values')
## 4. 残差图
residuals=y_test-y_pred
axes[1, 1].scatter(y_pred, residuals)
axes[1, 1].axhline(y=0, color='r', linestyle='--')
axes[1, 1].set_title('Residual Plot')
axes[1, 1].set_xlabel('Predicted Values')
axes[1, 1].set_ylabel('Residuals')
plt.tight_layout()
plt.show()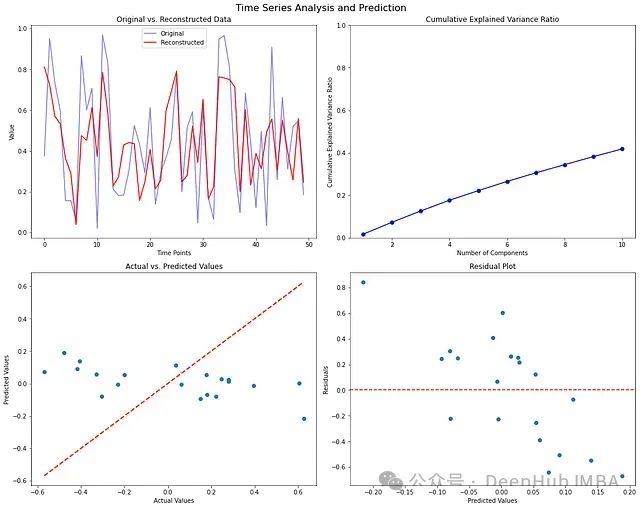
多图表分析:
解释方差比分析
- 累积方差比反映了信息保留程度
- 拐点可用于确定最优特征数量
- 通常在 90%处截断较为合理
预测性能评估
- 散点图集中在对角线附近表示预测准确
- 残差图用于检测系统性偏差
- 残差的分布特征反映了模型假设的合理性
与其他时间序列分析方法对比
传统统计方法对比
ARIMA 模型
- 优势:适合单变量时间序列,模型解释性强
- 局限:难以处理高维数据,计算复杂度高
- 对比:MFLE 在处理多变量时更有效率
指数平滑法
- 优势:计算简单,适合短期预测
- 局限:无法捕获复杂的时间依赖关系
- 对比:MFLE 能够发现更深层的数据结构
深度学习方法对比
LSTM 网络
- 优势:能够学习复杂的时序依赖
- 局限:需要大量训练数据,计算资源消耗大
- 对比:MFLE 在计算效率和可解释性方面更具优势
时序自编码器
- 优势:能够学习非线性特征
- 局限:模型复杂,训练不稳定
- 对比:MFLE 提供了更简单且可解释的解决方案
总结
时间序列数据的高维特性和复杂的时间依赖关系使其分析具有挑战性。MFLE 通过结合矩阵分解和时间序列分析的优势,为这类问题提供了一个有效的解决方案。
通过对 MFLE 的深入理解和合理应用,可以在众多实际场景中获得良好的分析效果。未来随着算法的改进和计算能力的提升,MFLE 的应用范围将进一步扩大。
https://avoid.overfit.cn/post/dc346136572240628a6bc3bfe77b5c95



