广义优势估计(Generalized Advantage Estimation, GAE)由 Schulman 等人在 2016 年的论文中提出,是近端策略优化(PPO)算法的重要基础理论,也是促使 PPO 成为高效强化学习算法的核心因素之一。
GAE 的理论基础建立在资格迹(eligibility traces)和时序差分 λ(TD-λ)之上,为深入理解 GAE 的核心价值,我们需要先分析其解决的根本问题。
强化学习中的核心问题
在策略梯度方法及广义强化学习框架中,信用分配问题(credit assignment problem)始终是一个关键挑战:当系统中的奖励延迟出现时,如何准确地判定哪些历史动作应当获得强化?
这一问题本质上是寻求偏差(bias)与方差(variance)之间的最佳平衡点。当算法考虑远期回报以强化当前动作时,会引入较大方差,因为准确估计真实期望回报需要大量采样轨迹。当算法仅关注短期回报时,会导致估计偏差增大,特别是当我们将状态价值估计为较小步数(如 TD 残差为 1 时)的 n 步回报加权平均时。
现有技术工具
在解决上述问题方面,强化学习领域已有资格迹和 λ-returns 等工具,以及 Sutton 与 Barto 在《强化学习导论》中详细讨论的 TD-λ 算法。而 λ-returns 方法需要完整的训练回合(episode)才能进行计算,传统 TD-λ 作为一个完整算法,直接将资格迹整合到梯度向量中。在 PPO 等现代算法中,我们期望将优势函数作为损失函数的一部分,这与 TD-λ 的直接应用方式不相兼容。
GAE 的技术创新
广义优势估计从本质上将 TD-λ 的核心思想引入策略梯度方法,通过系统性地估计优势函数,使其能够有效集成到算法损失函数中。回顾优势函数的定义,它计量特定动作价值与策略预期动作价值之间的差异,即衡量某动作相比于当前策略平均表现的优劣程度。
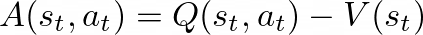
GAE 的工作原理
从直觉上理解,优势函数的构建需要准确评估状态-动作对的价值,以便测量其与状态价值函数或当前策略的偏差。由于无法直接获取真实值,需要构建既低方差又低偏差的估计器。GAE 采用 n 步优势的指数加权平均值方法,其中单个 n 步优势定义为:
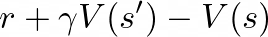
这些不同步长的优势估计各有特点:

上述估计中,TD(0)具有高偏差但低方差特性,而蒙特卡洛(MC)方法则表现为高方差低偏差。GAE 通过对各种不同步长优势估计的加权组合,实现了在 t 时刻的优势估计是状态或状态-动作价值的 n 步估计的衰减加权和。这种方法精确地实现了我们的目标:通过引入更精确的长期估计来减小偏差,同时通过适当降低远期估计权重来控制方差。
GAE 与 TD-λ 的技术区别
TD-λ 本质上是一个完整的算法,它以"反向"方式利用资格迹,使我们能够在每个时间步进行更新,该算法将资格迹直接整合到梯度更新中:
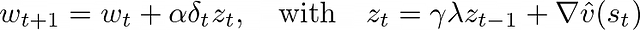
这一特性使 TD-λ 成为价值函数估计的有效工具,但在策略梯度方法中,我们需要自定义损失函数(如 PPO 中使用的损失函数),并且优化目标是策略而非价值函数。GAE 的创新之处在于找到了将这一思想应用于策略梯度方法的有效途径。
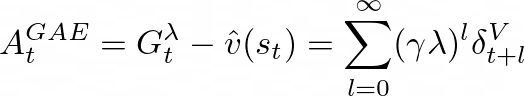
通过这种方式,GAE 可以作为损失函数中需要最小化的关键组件,为策略优化提供更稳定的梯度信号。
总结
本文通过系统分析明确了 GAE 的技术本质、理论来源以及其在当前强化学习领域最先进算法(尤其是 PPO)中的核心作用。GAE 通过巧妙平衡偏差与方差,为解决强化学习中的信用分配问题提供了一种数学严谨且实用高效的方法。
https://avoid.overfit.cn/post/dac142ef48c149d0bf30066535727cb0



