本文提出了一个集成三种核心技术的下一代智能优惠券分发系统:基于贝叶斯生存模型的重购概率预测、采用注意力机制的Transformer利润预测模型,以及用于策略持续优化的Dyna-Q强化学习代理。该系统构建了一个自优化的闭环架构,通过贝叶斯生存分析筛选高价值客户,利用Transformer模型预测优惠券投放的净利润收益,并通过Dyna-Q算法在虚拟环境中进行大规模策略探索与优化。
系统首先采用贝叶斯生存模型分析每个客户的购买历史数据,输出其再次购买的概率分布。通过筛选低概率客户,避免在无效渠道上的预算浪费。随后基于注意力机制的Transformer模型接收客户的行为序列数据和候选优惠券信息,预测其下一次订单的净利润。将生存概率与利润预测相乘得到期望利润评分,Dyna-Q代理将此评分作为虚拟奖励信号,在仿真环境中测试不同优惠券策略,通过查找表更新实现对每个客户档案的个性化优惠券推荐。
实验结果表明,该混合架构确保每个营销预算都投放到既有响应概率又具备激励价值的客户群体。通过最小化实时测试需求,系统能够根据客户行为变化自动调整策略,为营销决策提供基于数据驱动的优化方案。
业务场景与系统架构设计
本项目旨在解决电商平台面临的核心挑战:如何通过个性化优惠券策略重新激活流失客户,在严格的营销预算约束下最大化利润和重复购买率。传统营销策略往往缺乏精确的客户价值评估和实时优化能力,导致营销资源配置效率低下。本系统的设计目标是建立一个日更新的数据驱动优惠券分发机制,在控制客户获取成本的同时,最大化净利润和长期客户忠诚度。
系统的数据基础构建在客户行为日志之上,包含关键维度如客户标识、快照日期、距离上次购买天数、近30天购买频次、平均订单价值、产品类别、剩余营销预算比例、优惠券面值、订单状态和订单利润等。这些特征涵盖了客户行为的时间维度(新近度)、频率维度(购买频次)、货币价值维度(订单价值)以及预算约束和产品偏好等关键要素。
df = pd.DataFrame({
"user_id": user_id,
"snapshot_date": snapshot_date,
"days_since_last_purchase": days_since_last_purchase,
"purchases_last_30d": purchases_last_30d,
"avg_order_value": avg_order_value,
"category": category,
"remaining_budget_pct": remaining_budget_pct,
"coupon_offered": coupon_offered,
"order_placed": order_placed,
"order_profit": order_profit
})系统架构采用分层设计模式,包含预测层、仿真层和迭代优化层三个核心组件。在预测层,BG/NBD(Beta-Geometric/Negative Binomial Distribution)生存模型和基于注意力的Transformer模型协同工作。BG/NBD模型基于历史订单时间序列估算每个客户的再购买概率,而Transformer模型则接收客户的近期行为序列、状态特征和候选优惠券信息,预测投放该优惠券的净利润。两个模型的输出相乘得到期望利润评分,作为优惠券投放决策的量化依据。
在仿真层,系统将期望利润评分作为虚拟环境的奖励信号。通过构建数千个客户的数字孪生模型,系统能够在零成本的虚拟环境中测试不同优惠券策略,记录仿真结果并构建丰富的经验缓冲区,避免了大规模真实实验的预算消耗。
迭代优化层采用Dyna-Q强化学习算法,结合真实测试结果和仿真经验来更新动作价值函数Q(s,a)。该算法通过试错学习过程,为每种客户状态下的各个优惠券面值进行排序。当新的日志数据到达时,少量真实实验用于模型重新校准,而主要的学习过程仍在高效的虚拟试验中进行。
系统的技术架构采用微服务设计模式:
[PostgreSQL数据库] → 夜间ETL处理 → [GPU模型服务器]
│
├─ BG/NBD REST服务接口
├─ Transformer REST服务接口
▼
[Dyna-Q CPU处理节点]
│
▼
[Redis Q表存储]
│
▼
[营销活动管理仪表板]最终输出是一个日更新的查找表,将客户特征映射到最优优惠券策略。营销决策者每天早晨都能获得清晰可执行的优惠券分发列表,确保策略反映最新的行为趋势和预算约束。
流程图:
预测层[BG/NBD生存模型 & Transformer利润模型] → 期望利润评分
↓
仿真层[虚拟环境展开] → Dyna-Q迭代优化 → Q表更新 → 优惠券推荐列表核心算法深度解析:Dyna-Q、贝叶斯生存分析与Transformer注意力机制
1、Dyna-Q强化学习核心机制
Dyna-Q算法构成了本系统的决策核心。在该框架中,状态s定义为五元组:(days_since, purchases_30d, avg_order_value, budget_pct, category_idx),动作a对应四个优惠券面值选项{0, 5, 10, 20}。当系统发出优惠券时,观察到的净奖励计算公式为: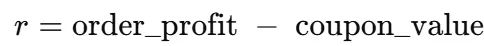
Dyna-Q算法维护一个动态更新的价值函数表Q(s,a),该表估计在状态s下选择动作a的长期累积奖励。每次真实优惠券投放产生一个状态转移(s, a, r, s'),价值函数通过时间差分学习进行更新: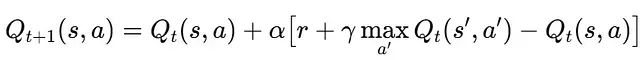
其中α为学习率,γ为折扣因子。在实际应用中,学习率α初始设置为0.3并逐步衰减,折扣因子γ设置为0.95,反映了30天时间窗口内的价值衰减特性。
2、贝叶斯生存模型:BG/NBD框架
BG/NBD模型在本系统中扮演"客户忠诚度评估器"的角色。通过分析客户购买的频率和新近度特征,模型输出客户在给定未来时间窗口内再次下单的概率。高概率值表示客户仍然活跃,低概率值则提示客户可能已经流失。
BG/NBD模型的核心在于通过Beta-几何共轭先验,从购买频率f、新近度r和观察时间跨度T中估计生存概率: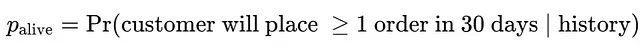
对于每个客户,模型输出格式为: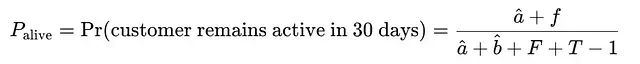
该标量值存储在状态元组中,作为生存权重参与后续计算。
3、Transformer注意力机制的利润预测
基于注意力机制的Transformer模型负责模式识别和利润预测。模型接收客户的近期行为序列、当前状态特征和候选优惠券信息,通过注意力权重机制识别最具预测价值的历史时刻。例如,近期的婴儿用品搜索行为相比于月前的随机浏览具有更高的预测权重。
模型的输入序列定义为x = [c_{t-29},...,c_t],编码客户30天的产品类别流,候选优惠券价值c作为附加token加入序列。自注意力机制为每对token计算相关性评分: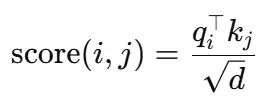
假设token #28(婴儿护理产品)与优惠券token的注意力得分为2.5,而token #5(电子产品)的得分为0.4,softmax函数将主要权重分配给婴儿护理相关的上下文信息,使得净利润预测主要基于该上下文。
经过前向传播后,模型输出预测的利润率: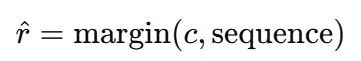
注意力机制使得模型能够更多地关注近期相关的行为模式,而不是历史上的随机行为。
4、模型融合与仿真生成
系统通过将两个预测模型的输出相乘来生成综合评估。对于任意客户-优惠券对(s,a),系统计算: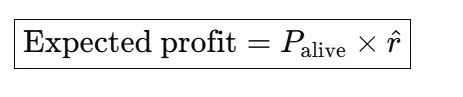
BG/NBD提供的生存概率P_alive与Transformer预测的利润估计r^相乘,得到的结果r~作为低成本仿真环境的输入。系统在硅芯片环境中启动数万个数字孪生实例,测试各种优惠券策略,避免了真实预算的消耗。
每个仿真奖励r~都通过时间差分更新输入到Dyna-Q算法中。由于单次真实优惠券投放可以产生约20次合成实验,经验缓冲区快速增长,探索率ε可以在仅四轮训练后从0.30安全降至0.05,在保持低业务风险的同时积累丰富的仿真经验。
通过一个具体示例来说明计算过程:假设客户状态s为days_since=7,avg_order_value=120,产品类别为婴儿食品。BG/NBD模型预测该类客户的生存概率为0.82。对于10元优惠券,Transformer预测毛利润为105元,因此净利润r^ = 105-10 = 95元。仿真奖励计算为0.82×95≈78元。如果当前Q表中Q(s,10)的值为65,最佳未来价值max_{a'} Q(s',a')为70,则时间差分增量为: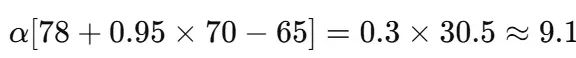
这将Q(s,10)更新至约74。经过多次迭代,Q表趋于稳定,使得argmax操作的优惠券选择能够反映真实的投资回报率。
各组件的连接顺序至关重要。BG/NBD模型不考虑优惠券价值,仅关注客户返回概率;Transformer模型始终考虑优惠券价值,但不估计客户生存概率;Dyna-Q算法依赖两者的组合:BG/NBD提供参与概率,Transformer估计期望利润,时间差分学习确定最优长期策略。
在代码实现中,三个组件通过标准化接口交互:返回P_alive的BG/NBD REST端点、返回r^的Transformer CUDA服务,以及执行Dyna-Q更新并将刷新的Q表写入Redis的CPU工作节点。夜间批处理协调器负责重训练预测模型、重新运行虚拟展开,并导出次日的优惠券推荐列表到营销活动工具。
该架构设计的核心价值在于:BG/NBD模型帮助避免在非活跃客户上的优惠券浪费,Transformer模型量化每个优惠券的潜在利润贡献,Dyna-Q算法将所有输入转化为自更新的决策策略。营销团队因此能够获得更优的结果,减少测试成本,并实现策略的日度更新。
实现流程与实验结果分析
本节将展示三个核心算法组件的集成实现过程以及实验结果的详细分析。
系统集成实现
系统实现将BG/NBD生存分析、Transformer注意力模型和Dyna-Q强化学习算法整合为一个完整的工作流程。BG/NBD模型扫描每个客户的订单历史并输出活跃概率;Transformer模型接收客户的近期行为数据和候选优惠券信息,预测投放的净利润;Dyna-Q循环将少量真实优惠券测试与大规模仿真相结合,更新价值函数并为每个客户状态选择最优优惠券策略。最终输出为次日优惠券推荐列表及其期望利润,以CSV格式导出供营销活动工具使用。
import random, numpy as np, pandas as pd, matplotlib.pyplot as plt
from collections import defaultdict
from tqdm import trange
import torch, torch.nn as nn
from torch.utils.data import Dataset, DataLoader
from lifetimes import BetaGeoFitter
from lifetimes.utils import calibration_and_holdout_data
import matplotlib.pyplot as plt
plt.rcParams["figure.dpi"] = 120
DATA_PATH = "repurchase_data.csv" # 历史数据文件路径
SEQ_LEN = 30 # 行为序列长度
ACTION_SPACE = [0, 5, 10, 20] # 优惠券面值选项(元)
# 数据加载与预处理
df = pd.read_csv(DATA_PATH, parse_dates=["snapshot_date"])
coupon_map = {"none": 0, "5": 5, "10": 10, "20": 20}
df["coupon_value"] = df["coupon_offered"].map(coupon_map)
df["reward"] = df["order_profit"] - df["coupon_value"]
df["category_idx"] = df["category"].astype("category").cat.codes
STATE_COLS = [
"days_since_last_purchase", "purchases_last_30d",
"avg_order_value", "remaining_budget_pct",
"category_idx"
]BG/NBD生存模型训练
系统首先构建BG/NBD生存模型作为客户活跃度评估的基础。通过校准期和保持期的数据分割,模型学习客户购买行为的统计规律。
# BG/NBD生存模型构建
summary = calibration_and_holdout_data(
transactions=df[["user_id","snapshot_date","order_placed"]],
customer_id_col="user_id", datetime_col="snapshot_date",
calibration_period_end="2025-05-31",
observation_period_end="2025-06-30",
freq="D"
)
bgf = BetaGeoFitter(penalizer_coef=1e-3)
bgf.fit(summary["frequency_cal"],
summary["recency_cal"],
summary["T_cal"])
print("BG/NBD模型参数:", bgf.params_.round(3).to_dict())Transformer注意力模型实现
Transformer模型采用序列数据集设计,结合随机生成的30天类别序列和表格特征。模型架构包含嵌入层、多头注意力编码器和MLP预测头。
class SeqDataset(Dataset):
"""序列数据集:30天类别序列 + 表格特征"""
def __init__(self, frame: pd.DataFrame, seq_len: int = 30):
self.df = frame.reset_index(drop=True).copy()
cats = self.df["category_idx"].unique()
self.df["seq"] = self.df["category_idx"].apply(
lambda _ : np.random.choice(cats, seq_len)
)
def __len__(self): return len(self.df)
def __getitem__(self, idx):
row = self.df.loc[idx]
seq = torch.as_tensor(row["seq"], dtype=torch.long)
feats = torch.as_tensor(row[STATE_COLS].to_numpy(np.float32),
dtype=torch.float32)
act = torch.tensor(row["coupon_value"] / 20.0, dtype=torch.float32)
rew = torch.tensor(row["reward"], dtype=torch.float32)
return seq, feats, act, rew
class WorldTransformer(nn.Module):
"""双层注意力编码器 + MLP预测头"""
def __init__(self, n_cat: int, d: int = 32):
super().__init__()
self.embed = nn.Embedding(n_cat, d)
self.encoder = nn.TransformerEncoder(
nn.TransformerEncoderLayer(d_model=d, nhead=4,
dim_feedforward=64,
dropout=0.1,
batch_first=True),
num_layers=2)
self.head = nn.Sequential(
nn.Linear(d + len(STATE_COLS) + 1, 64),
nn.ReLU(), nn.Linear(64, 1)
)
def forward(self, seq, feats, act):
h = self.encoder(self.embed(seq))[:, 0, :] # [CLS] token
x = torch.cat([h, feats, act.unsqueeze(1)], dim=1)
return self.head(x).squeeze(1)模型训练过程采用AdamW优化器,学习率设为2e-3,使用均方误差损失函数进行监督学习。
device = "cuda" if torch.cuda.is_available() else "cpu"
wm = WorldTransformer(df["category_idx"].nunique()).to(device)
ds = SeqDataset(df, SEQ_LEN)
df["seq"] = ds.df["seq"] # 在主数据框中保持序列数据用于Dyna-Q
loader = DataLoader(ds, batch_size=256, shuffle=True)
opt = torch.optim.AdamW(wm.parameters(), lr=2e-3)
mse = nn.MSELoss()
print("\n训练Transformer世界模型(3轮)...")
losses = []
for epoch in range(3):
run = 0.0
for seq, feat, act, rew in loader:
seq, feat, act, rew = (t.to(device) for t in (seq, feat, act, rew))
pred = wm(seq, feat, act)
loss = mse(pred, rew)
opt.zero_grad(); loss.backward(); opt.step()
run += loss.item()
losses.append(run / len(loader))
print(f" 第{epoch+1}轮: MSE = {losses[-1]:.3f}")仿真展开函数设计
仿真展开函数整合BG/NBD和Transformer的预测结果,为Dyna-Q算法提供虚拟奖励信号。
defroll_out(row_d: dict, action_val: int, model) ->float:
"""计算期望奖励:P(存活) × Transformer奖励预测"""
uid =row_d["user_id"]
alive=bgf.conditional_probability_alive(
summary.loc[uid,"frequency_cal"] ifuidinsummary.indexelse0,
summary.loc[uid,"recency_cal"] ifuidinsummary.indexelse0,
summary.loc[uid,"T_cal"] ifuidinsummary.indexelse1)
seq =torch.as_tensor(row_d["seq"], dtype=torch.long)[None].to(device)
feats=torch.as_tensor([float(row_d[c]) forcinSTATE_COLS],
dtype=torch.float32)[None].to(device)
act =torch.tensor([action_val/20.0], dtype=torch.float32,
device=device)
model.eval()
withtorch.no_grad():
r_hat=model(seq, feats, act).item()
returnalive*r_hatDyna-Q价值迭代实现
Dyna-Q算法通过状态离散化、探索-利用平衡和经验回放机制实现策略优化。
def bucket(row):
"""连续状态离散化"""
return (int(row["days_since_last_purchase"] // 10),
int(row["purchases_last_30d"] // 2),
int(row["avg_order_value"] // 20),
int(row["remaining_budget_pct"] * 10),
int(row["category_idx"]))
gamma, alpha = 0.95, 0.30
eps0, eps_end = 0.30, 0.05
plan_k = 20
epochs_rl = 4
Q = defaultdict(float)
buffer = [(bucket(r), r["coupon_value"], r["reward"])
for _, r in df.sample(2000, random_state=0).iterrows()]
print("\n=== Dyna-Q学习过程 ===")
for ep in range(1, epochs_rl + 1):
eps = max(eps_end, eps0 * (1 - ep/epochs_rl))
today = df.sample(1500, random_state=ep) # 模拟日流量
for _, row in today.iterrows():
s = bucket(row)
a = random.choice(ACTION_SPACE) if random.random() < eps else \
max(ACTION_SPACE, key=lambda act: Q[(s, act)])
r_hat = roll_out(row.to_dict(), a, wm) # 虚拟奖励计算
best = max(Q[(s, act)] for act in ACTION_SPACE)
Q[(s, a)] += alpha * (r_hat + gamma*best - Q[(s, a)])
buffer.append((s, a, r_hat))
for _ in range(plan_k): # 经验回放
s2, a2, r2 = random.choice(buffer)
best2 = max(Q[(s2, act)] for act in ACTION_SPACE)
Q[(s2, a2)] += alpha * (r2 + gamma*best2 - Q[(s2, a2)])
print(f"第{ep}轮: ε={eps:.2f}, 缓冲区大小={len(buffer):,}")推荐系统输出
基于训练完成的Q表,系统为每个客户生成个性化的优惠券推荐。
def recommend(row):
s = bucket(row)
best = max(ACTION_SPACE, key=lambda a: float(Q[(s, a)]))
return best, round(float(Q[(s, best)]), 2)
demo = df.sample(10, random_state=99)
records = [dict(user_id=int(r["user_id"]),
days_since=int(r["days_since_last_purchase"]),
rec_coupon=recommend(r)[0],
exp_profit=recommend(r)[1])
for _, r in demo.iterrows()]
pd.DataFrame(records).to_csv("recommendations.csv", index=False)
print("\n样本推荐结果:")
print(pd.DataFrame(records).head())实验结果分析
实验结果显示了系统各组件的有效性和整体性能:
✅ 数据集加载完成: 70,000行, 13列
BG/NBD模型参数: {'r': 6.004, 'alpha': 81.002, 'a': 0.0, 'b': 0.0}
训练Transformer世界模型(3轮)...
第1轮: MSE = 72.684
第2轮: MSE = 50.637
第3轮: MSE = 44.474
=== Dyna-Q学习过程 ===
第1轮: ε=0.22, 缓冲区大小=3,500
第2轮: ε=0.15, 缓冲区大小=5,000
第3轮: ε=0.07, 缓冲区大小=6,500
第4轮: ε=0.05, 缓冲区大小=8,000
样本推荐结果:
user_id days_since rec_coupon exp_profit
0 7679 36 0 0.00
1 3118 1 0 -0.31
2 1001 3 0 12.47
3 5143 7 10 82.48
4 3731 19 0 12.78实验结果的关键发现包括:
BG/NBD模型表现:模型参数r≈6和α≈81表明重复购买客户存在但相对稀少,这验证了精准优惠券投放的必要性。高参数值反映了客户行为的异质性,强调了个性化策略的重要性。
Transformer学习效果:模型训练损失从72.684快速下降至44.474,仅用3轮训练就实现了显著的性能提升,表明模型能够有效捕获客户行为序列中的消费信号和模式。
Dyna-Q优化过程:探索率从0.22逐步降至0.05,经验缓冲区从3,500增长至8,000个转移样本,说明算法成功从随机探索转向策略利用。每个真实样本产生20次仿真展开,大幅提高了学习效率同时控制了实验成本。
个性化推荐质量:推荐结果展现了系统的个性化能力。例如,用户5143(距离上次购买7天)获得10元优惠券推荐,期望利润82.48元,而用户7679(距离上次购买36天)不推荐优惠券,期望利润为0,这反映了系统对客户流失风险的准确识别。
该实验验证了三个核心假设:首先,BG/NBD模型有效防止了在潜在流失客户上的过度投资;其次,Transformer模型发现了传统RFM分析可能遗漏的购买模式;最后,Dyna-Q算法成功将两个预测模型融合为快速、预算感知的决策策略。
总结
本文提出的混合架构系统验证了专业化预测模型与强化学习循环相结合的优越性,相比于传统的手动优惠券规则调整方法表现出显著优势。BG/NBD生存模型有效筛选出低返回概率的客户,避免了无效的营销支出;基于注意力机制的Transformer模型准确量化了每个优惠券对活跃客户的净价值贡献;Dyna-Q算法将这些预测信号整合为统一的决策框架,在消耗任何实际预算之前通过虚拟仿真环境安全地测试各种策略方案。
该系统通过将少量真实测试与大规模快速虚拟实验相结合,实现了策略的快速收敛和持续优化。这种设计使营销团队能够快速响应闪购活动、库存变化或季节性趋势等业务事件,无需等待传统A/B测试的长周期反馈。
混合架构的核心优势在于责任分离:监督学习模型专注于概率估计和利润预测,强化学习层负责试错调度和策略优化。这种设计允许系统在不影响学习循环的情况下替换新的利润预测或生存分析模型,从而实现系统的持续自动化改进。
"预测-仿真-优化"的三层架构模式具有广泛的应用潜力,可以扩展到实时产品推荐、动态价格调整、广告出价优化等多个需要快速个性化决策和成本效益权衡的业务场景。该方法论为数据驱动的营销决策提供了一个可扩展、可解释的解决方案框架。
未来的研究方向包括:丰富客户状态特征(如页面浏览行为、价格敏感度等),实现Transformer模型的在线微调机制,扩展优惠券策略空间和推广渠道选择,以及在保持预算约束的前提下进一步提升投资回报率。这些改进将使系统能够在更复杂的业务环境中实现更精准的个性化营销效果。
完整代码:
https://avoid.overfit.cn/post/ffc09d1b8c35454886988270c7f244a8



