在本文中先破除大家对神经元的一些误解和心理障碍。并手工写一个神经元。
《神经网络实战》系列专栏持续更新介绍神经元怎么工作,最后使用python从0到1不调用任何依赖库(不使用scipy和tensorflow和numpy)来实现神经网络。
作者:司南牧
逻辑与(AND)
我们先不管什么是神经元,咱们先介绍下逻辑与(AND)是什么。在计算机中,存储的是0和1。计算机有很多对这种01操作的运算,其中有一种运算叫做逻辑与,在编程中运算符通常表示为&。两个数进行逻辑与运算的规则就是只要有一个数是0,那么整个运算就是0。还是不太懂?我们举个例子。
1&0 == 0
0&1 == 0
0&0 == 0
1&1 == 1
然后我们要解决的问题是,怎么让神经元根据这四组数据自己学习到这种规则。接下来我们整理下这四个数据。然后我们将x1&x2==y的四种情况可以表示为如下所示。我们需要做的是让一个神经元根据这四个数据学习到逻辑与的规则。
x1 x2 y
1 0 0
0 1 0
0 0 0
1 1 1
也就是说,将(x1,x2)视作一个坐标,将它描点在二维平面是这样的。
我们让神经元能够学习到将(0,1)、(0,0)、(1,0)这些点分类为0,将(1,1)这个点分类为1。更直观的讲就是神经元得是像图中的这条直线一样,将四个点划分成两类。在直线左下是分类为0,直线右上分裂为1.
破除神经元的认知障碍
在人工智能范畴的的神经元它本质是一条直线,这条直线将数据划分为两类。与生物意义上的神经元可谓是千差万别。你可以理解为它是受到生物意义上的神经元启发,然后将它用来形象化数学公式。
既然神经元它在数学意义上就是一条直线那么,怎么表示呢?
学计算机一个很重要的思维就是:任何一个系统都是由输入、输出、和处理组成。
我们在了解神经元也是一样,在本文中的需求是知道一个坐标(x1,x2),输出这个坐标的分类y。
我们按照计算机的输入输出思维整理下思路:
输入:x1,x2输出:y处理:自己学习到从x1,x2到y的一种映射方法
我们知道输入输出,并且我们知道它是直线,那么我们就可以描述这个问题了。
我们让神经元能够学习到将(0,1)、(0,0)、(1,0)这些点分类为0,将(1,1)这个点分类为1。更直观的讲就是神经元得是像图中的这条直线一样,将四个点划分成两类。在直线左下是分类为0,直线右上分裂为1.
我们继续看这个图,在直线的右上方是x1&x2==1的情况,即分类为1的情况。在直线左下是x1&x2==0的情况。这个时候就可以用我们高中的知识来解决这个问题了。在高中我们知道一条直线可以表示为。由于啊,在神经元里面大家喜欢把前面的系数叫做权重(weight),把常数项叫做偏置(bias)。因此一般大家把前面系数命名为,把常数项命名为。这些都是约定俗成,所以大家记忆下就好。在本文中,我用下面这个公式表示图中的那条绿色的直线。
根据高中知识,一条直线将平面划分成两半,它可以用如下方式来描述所划分的两个半平面。
- 左下:,当和至少有一个是0 的时候。
- 右上:,当和都是1 的时候。
其实,就是神经元,一个公式而已。是不是觉得神经元的神秘感顿时消失?大家平常看到的那种图只不过是受生物启发而画的,用图来描述这个公式而已。我们画个图来表示神经元,这种画图方法是受到生物启发。而求解图中的参数则从来都是数学家早就知道的方法(最小二乘法)。
然后,前面提到过,神经元的形象化是受到生物启发。所以我们先介绍下怎么启发的。
生物意义上的神经元,有突触(输入),有轴突(输出),有细胞核(处理)。并且神经元传输的时候信号只有两个正离子和负离子。这和计算机1和0很类似。
总结下,神经元有突触(输入),有轴突(输出),有细胞核(处理)。开工画图:
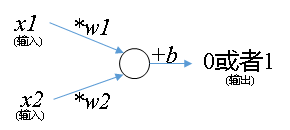
咱们把上面这个神经元的数学表达式写一下对比下,.以后啊,大家见到神经元就用这种方式理解就可以。大家不要对神经网络过于迷信化和模糊化,它不是玄学。神经元不是玄学,不是艺术(我只是那种感性经验思维),它是数学和生物启发结合的产物。
好现在我们知道神经元的数学表达和怎么画它的形象化的图了。那么不如我们用编程也表达下它吧?
实践:用程序表示一个手工设置权重weight和偏置bias的神经元
去掉注释就10行左右的代码,好现在自己动手实践下吧?计算机思维:动手写代码进行实践是进步的唯一方法
# -*- coding: utf-8 -*-
"""
让神经元学习到逻辑与这个规则
@author: 李韬_varyshare
"""
class Neuron(object):
def __init__(self):
"""
手工设置神经元的权重w_i(输入x_i前面的系数),和偏置常数项b=-1.1
"""
# 初始化权重数组,假定weights[i]和公式中的wi一一对应
self.weights = [1.0,1.0]
# 偏置也初始化为0
self.bias = -1.1
def f(self,x0,x1):
"""
返回值是 weights[0]*x0+weights[1]*x1 + bias > 0? 1:0;
计算这个用于判断(x0,x1)的分类。大于0则是点(x0,x1)在右上输出1,小于0则点在左下输出0;
"""
if self.weights[0]*x0+self.weights[1]*x1 + self.bias > 0:
return 1
else:
return 0
# 哈哈我们手工设置了一个神经元能完美实现逻辑与
n = Neuron()
# 0&1==0
print('0&1=',n.f(0,1))
# 1&0==0
print('1&0=',n.f(1,0))
# 0&0==0
print('0&0=',n.f(0,0))
# 1&1 == 1
print('1&1=',n.f(1,1))
"""
输出:
0&1= 0
1&0= 0
0&0= 0
1&1= 1
"""
那么怎么让计算机自己确定神经元的参数?
现在问题来了,现在我们有三个参数,我们怎么设置这三个参数呢?一个很直观的想法就是自己手动调。
别笑,还真可以。因为我们现在要解决的问题太简单了。一个很直观的解就是只要直线的斜率为-1,即.然后我们让b=-1.1就可以完美实现逻辑与分类功能。也就是说这就是一个符合条件的神经元。
好了,可以洗洗睡散了。
但是,通常我们要解决的问题比这个复杂的多,神经网络是由神经元连接而成。而一般神经网络都是有几百个神经元。假设有200个神经元,我们现在一个神经元有3个参数,那么我们手动需要调200*3=600个参数。想想都觉得头皮发麻,而且200个神经元这还算少的,AlphaGo那种级别得上千个。恐怖如斯。
梯度下降
当然,数学家不会这么傻乎乎的自己手动调。数学家想到了一个办法叫做梯度下降。大家不知道这个方法没关系,现在你需要知道的是梯度下降可以让计算机自动调节我们设置的参数就可以了。
那梯度下降怎么做的呢?
剩下内容本专栏后续文章会继续更新。
欢迎关注我的知乎专栏适合初学者的机器学习神经网络理论到实践。
第一篇为零基础神经网络实战(1):单个神经元+随机梯度下降学习逻辑与规则
第二篇为适合初学者的神经网络理论到实践(2):理解并实现反向传播及验证神经网络是否正确
第三篇为适合初学者的神经网络理论到实践(3):打破概念束缚:强化学习是个啥?



