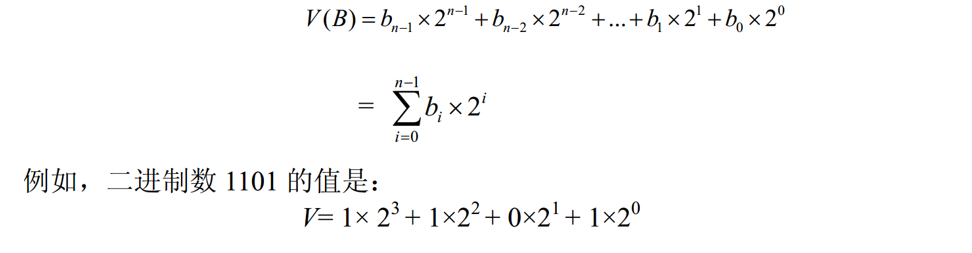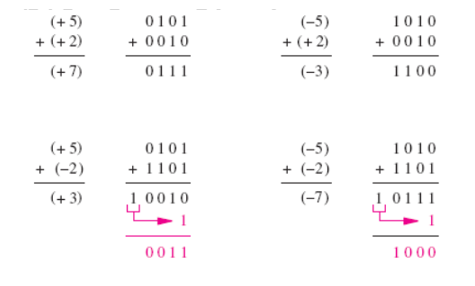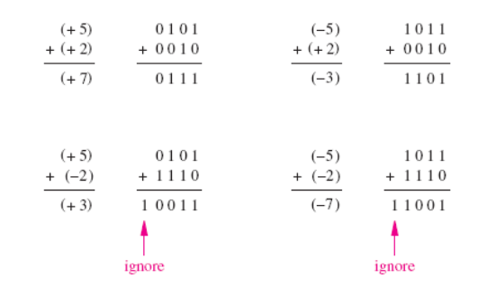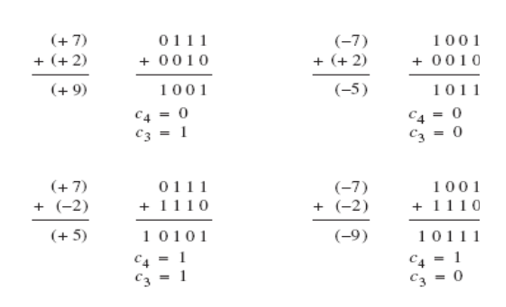十进制数大家都很熟悉,既方便又易于理解,但是在数字电路中十进制数就不太好办了。在数字系统中我们使用的是只由0和1两个数字构成的二进制数,或者叫作基2的数。每个二进制数位叫作一个位(bit)。
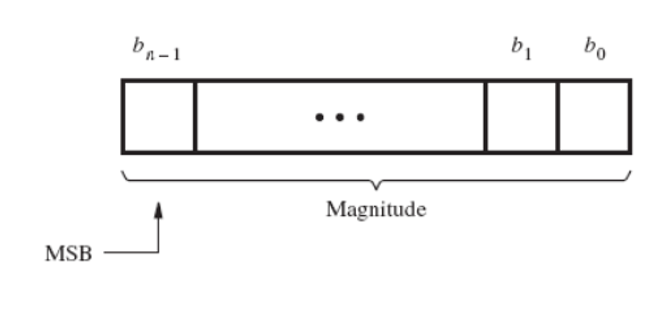
在无符号数中所有的位都代表了数的大小,因此在定义数的大小时,所有n位都是有意义的。因此最高位(MSB)就是无符号整数的最左侧的位bn-1。
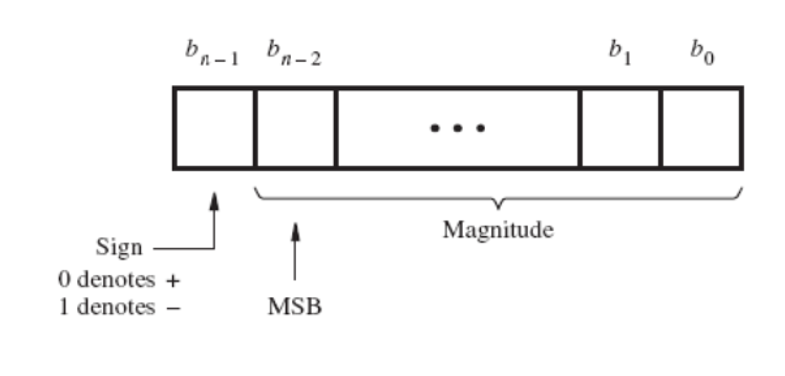
在十进制系统中将“+”或“-”标在最高有效位的左侧来表示数的正负,而在二进制系统中,数的符号是由其最左侧的位来决定的。正数的最左侧位为0,负数为1。因此,有符号数的最左侧位代表了它的符号,而余下的n-1位代表了它的大小。在有符号数中,有 n-1个有意义的位,最高位(MSB)是 bn-2。
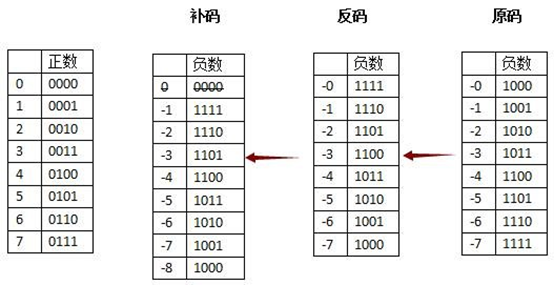
在数字IC中有符号二进制数可以有三种表示方法:原码、反码和补码
原码:
在原码中分别用符号位为“0”或者为“1”来分别表示数的正、负。例如,四位二进制数正负5,可以分别用+5=0101 和-5=1101来表示。由于与十进制数有符号数表示十分相似,因此这种表示法很容易理解,然而这种表示方法并不适用于计算机的应用。
反码:
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变,其余各个位取反.
补码:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
下面我们将使用由一个符号位和三个数值位组成的四位数说明不同数值表示法的优劣势。这些数必须足够小,以至它们和的数值才能用3位数来表示,也就是说它们和的数值不能大于 7。
计算正数加法使用三种表示法都一样,与无符号数的加法是相同的。但是对于负数来说却有很显著的不同。
原码表示法的加法运算
若两个相加的数符号相同,则两个用原码表示法的数的相加是很简单的:大小相加,符号不变。但是如果两个加数异号,情况就复杂了一些。这就需要从大数里减去小数,意味着逻辑电路必须要有比较和减法的操作,在计算机中并不适合使用原码表示法。
反码表示法的加法运算
下图展示了两个反码表示法的数相加的情况。
两个数相加共有四种不同的符号组合。从图的上半部分来看计算5+2 = 7 和 -5+2= 3 十分简单,将两个加数简单相加即可。但计算其它两种组合就不那么简单了。计算5+ (-2) = 3 产生位向量10010。由于我们处理的是四位数,从符号位会有进位,而且最后得到2而不是正确的结果3。有趣的是,如果我们将符号位的进位加到结果的最低有效位上,得到的就是正确结果3。当计算(-5)+ (-2) = 7时遇到的是同样的问题,最先得到的是错误结果0111,表示的是7而不是-7,我们使用同样的纠正该方法将符号位的进位加到其最低有效位(LSB)上。
由这些例子得到的结论是使用反码有时很方便,但有时不方便。若遇到需要纠正的情况,则必须要再做一次加法。因此,两个反码表示法的加法运算所花费的时间也许是两个无符号数相加所花费时间的两倍。
补码表示法的加法运算
在补码表示法的加法例子中使用相同的加数组合。
5+2 =7 和 -5+2=3 很简单。5+(- 2) = 3 和(-5) + (-2) = (-7)也得到了正确的结果,从符号位产生的进位我们尽可以忽略。
由这些例子可以看出,补码表示法的加法运算十分简单。不论操作数的符号是什么,结果总是正确的。如果有进位,直接将它忽略就可以了。补码表示法的加法运算可以由一个加法器电路来实现,所以非常适合于加法电路应用的。
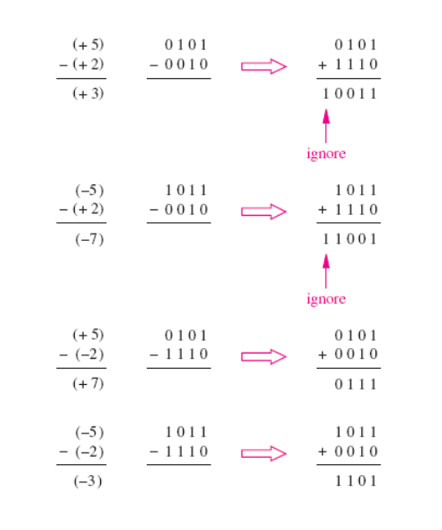
下面我们将考虑它在减法操作中的应用,具体关系如下
A补-B补=A补+(-B)补
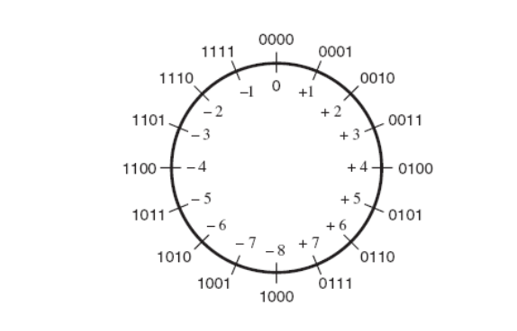
我们可以把所有的四位数的补码放在下图一个模十六的圆上
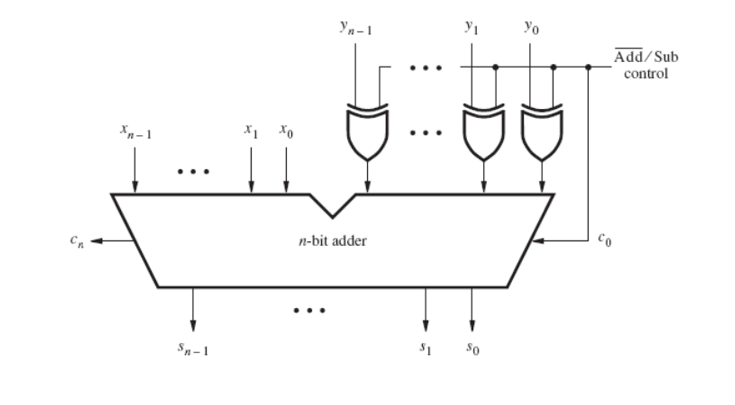
然后通过同一个电路实现加减法
前面假定加法的运算结果的位数都在数的有效表示范围之内。若用n位表示一个有符号数, 则运算结果必须在-2n-1到2 1 n-1 - 范围之内。若结果超出此范围,则说算术运算发生溢出。为了保证算术运算电路能正确地工作,电路中必须有能够检测是否发生溢出的机制。
当两个数的符号不同时,则加法运算不会发生溢出,当两个数的符号相同时,则加法运算可能会发生溢出。
从上图可以看出,判断溢出的机制关键在于c3和c4的取值是否相同
由此可知,若我们上图电路稍作修改,添加一个异或门,便可以指示是否发生算术溢出。
本文转载自公众号:芯片数字实验室
原文链接:https://mp.weixin.qq.com/s/gFmz2fvl5YkG8Npi9\_sjuw
未经作者同意,请勿转载!
推荐阅读
- 硬件算法优化,做一个不被EDA工具替代的IC Designer
- Cell延时从哪里来?非线性延时模型(NLDM)把一切都告诉你
- 基于QuestaSIM的SystemVerilog DPI使用流程(step by step)
想了解更多内容,欢迎关注芯片数字实验室专栏,由于工具,你可以专注在更重要的事情上。